题目内容
17.如果|x|≤$\frac{\sqrt{2}}{2}$,那么函数y=-x2+x+1的最小值是( )| A. | $\frac{\sqrt{2}-1}{2}$ | B. | $\frac{\sqrt{2}+1}{2}$ | C. | -1 | D. | $\frac{1-\sqrt{2}}{2}$ |
分析 因为y=-x2+x+1开口向下,对称轴x=$\frac{1}{2}$,在对称轴左侧,y随着x的增大而增大,在对称轴右侧,y随着x的增大而减小,再由|x|≤$\frac{\sqrt{2}}{2}$,得出-$\frac{\sqrt{2}}{2}$≤x≤$\frac{\sqrt{2}}{2}$,代入两个最低点,比较得出答案即可.
解答 解:∵y=-x2+x+1的-1<0,
∴开口向下,对称轴x=$\frac{1}{2}$,
∵|x|≤$\frac{\sqrt{2}}{2}$,
∴-$\frac{\sqrt{2}}{2}$≤x≤$\frac{\sqrt{2}}{2}$,
∴左侧最低点y=-(-$\frac{\sqrt{2}}{2}$)2+(-$\frac{\sqrt{2}}{2}$)+1=$\frac{1-\sqrt{2}}{2}$,
右侧最低点y=-($\frac{\sqrt{2}}{2}$)2+$\frac{\sqrt{2}}{2}$+1=$\frac{\sqrt{2}+1}{2}$,
∵$\frac{1-\sqrt{2}}{2}$<$\frac{\sqrt{2}+1}{2}$,
∴|x|≤$\frac{\sqrt{2}}{2}$,那么函数y=-x2+x+1的最小值是$\frac{1-\sqrt{2}}{2}$.
故选:D.
点评 此题考查二次函数的最值,掌握二次函数的性质,求得对称轴是解决问题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
8.填表:
| 多边形的边数 | 7 | 17 | 20 | 25 |
| 内角和 | 5×180° | 15×180° | 18×180° | 23×180° |
| 外角和 | 360° | 360° | 360° | 360° |
6.已知直角三角形的两边长是3和5,则此三角形的第三边长是( )
| A. | 4 | B. | $\sqrt{34}$ | C. | 4或$\sqrt{34}$ | D. | 以上都不对 |
 如图所示,在六边形ABCDEF中,AF∥CD,AB∥DE,BC∥EF,且∠A=120°,∠B=80°,试求六边形其余各角的度数.
如图所示,在六边形ABCDEF中,AF∥CD,AB∥DE,BC∥EF,且∠A=120°,∠B=80°,试求六边形其余各角的度数.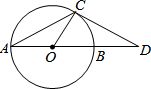 如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°.判断DC是否为⊙O的切线,并说明理由.
如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°.判断DC是否为⊙O的切线,并说明理由.