题目内容
5. 如图所示,在六边形ABCDEF中,AF∥CD,AB∥DE,BC∥EF,且∠A=120°,∠B=80°,试求六边形其余各角的度数.
如图所示,在六边形ABCDEF中,AF∥CD,AB∥DE,BC∥EF,且∠A=120°,∠B=80°,试求六边形其余各角的度数.
分析 分别延长AF、DE交于点G,延长AB、DC交于点H,可证得四边形AGDH为平行四边形,可得∠D=∠A.分别延长FA、CB交于点M,延长FE、CD交于点N,
四边形FMCN为平行四边形,可得∠AFN=∠MCN,∠M+∠AFN=180°,所以∠AFN=∠MCN=180°-∠M=180°-12°=168°,再利用六边形的内角和,即可求出∠DEF.
解答 解:如图,分别延长AF、DE交于点G,延长AB、DC交于点H;分别延长FA、CB交于点M,延长FE、CD交于点N,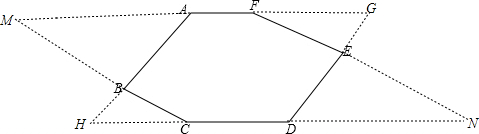
∵AF∥CD,AB∥DE,
∴四边形AGDH为平行四边形,
∴∠FAB=∠CDE=120°,
∵∠FAB=120°,
∴∠MAB=180°-∠FAB=60°,
∵∠ABC=80°,
∴∠M=∠ABC-∠MAB=80°-60°=20°,
∵AF∥CD,BC∥EF,
∴四边形FMCN为平行四边形,
∴∠AFN=∠MCN,∠M+∠AFN=180°,
∴∠AFN=∠MCN=180°-∠M=180°-20°=160°,
六边形的内角和为:(6-2)×180°=720°,
∴∠DEF=720°-∠FAB-∠ABC-∠BCD-∠CDE-∠AFE=80°.
点评 本题主要考查平行四边形的判定和性质,掌握两组对边分别平行的四边形为平行四边形是解题的关键.

练习册系列答案
相关题目
16.下列四个式子中错误的是( )
| A. | -1>-2 | B. | -3.5>-4 | C. | -5>-5 | D. | -0.21>-0.211 |
17.如果|x|≤$\frac{\sqrt{2}}{2}$,那么函数y=-x2+x+1的最小值是( )
| A. | $\frac{\sqrt{2}-1}{2}$ | B. | $\frac{\sqrt{2}+1}{2}$ | C. | -1 | D. | $\frac{1-\sqrt{2}}{2}$ |
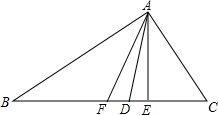 如图:∵AD是△ABC的角平分线.∴∠BAD=∠DAC=$\frac{1}{2}$∠BAC(或:∠BAC=2∠BAD=2∠DAC)
如图:∵AD是△ABC的角平分线.∴∠BAD=∠DAC=$\frac{1}{2}$∠BAC(或:∠BAC=2∠BAD=2∠DAC) 如图,已知线段AB,用直尺和圆规,以AB为底边作等腰三角形ABC,使高CD=AB.(不要写作法,保留作图痕迹)
如图,已知线段AB,用直尺和圆规,以AB为底边作等腰三角形ABC,使高CD=AB.(不要写作法,保留作图痕迹)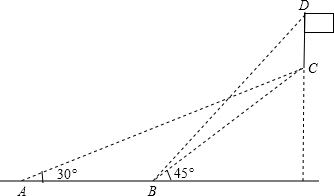
 已知:四边形ABCD中,$\frac{AB}{AE}=\frac{AC}{AD}=\frac{BC}{ED}$.求证:△ADC∽△AED.
已知:四边形ABCD中,$\frac{AB}{AE}=\frac{AC}{AD}=\frac{BC}{ED}$.求证:△ADC∽△AED.