题目内容
19. 如图,AB为⊙O的直径,ED切⊙O于点C,过点A作AF⊥ED于点F,交⊙O于点G,连接AC;
如图,AB为⊙O的直径,ED切⊙O于点C,过点A作AF⊥ED于点F,交⊙O于点G,连接AC;(1)猜想线段AC、AB与AF之间的数量关系,并证明你的结论;
(2)如果CF=4,GF=2,求⊙O的半径.
分析 (1)连结BC、OC,然后依据切线的性质可知OC⊥DE,从而可证明OC∥AF,然后依据平行线的性质和等腰三角形的性质可证明∠BAC=∠CAF,故此可证明△ABC∽△ACF,依据相似三角形的性质可得到线段AC、AB与AF之间的数量关系;
(2)连结OC、CG,然后证明△CGF∽△ACF,依据相似三角形的性质可求得AF的长,依据勾股定理可求得AC的长,然后依据(1)中的结论求解即可.
解答 解:(1)AC2=AB•AF.
理由:如图所示:BC、OC.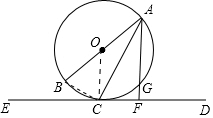
∵ED切⊙O于点C,
∴OC⊥DE.
∵AF⊥ED,
∴OC∥AF.
∴∠OCA=∠CAF.
∵OC=OA,
∴∠OCA=∠OAC.
∴∠BAC=∠CAF.
∵AB为⊙O的直径,
∴∠BCA=90°.
∴∠BCA=∠CFA.
∴△ABC∽△ACF.
∴$\frac{AB}{AC}=\frac{AC}{AF}$,即AC2=AB•AF.
(2)连结OC、CG.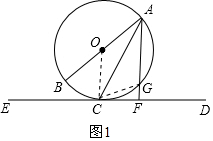
∵DE为⊙O的切线,
∴∠GCF=∠CAF.
又∵∠AFC=∠CFG.
∴△CGF∽△ACF,
∴$\frac{AF}{CF}=\frac{CF}{FG}$,AF=$\frac{C{F}^{2}}{FG}$=8.
在Rt△ACF中,依据勾股定理可求得AC=4$\sqrt{5}$.
由(1)可知:AB=$\frac{A{C}^{2}}{AF}$=$\frac{80}{8}$=10.
∴OA=OB=5.
∴⊙O的半径为5.
点评 本题主要考查的是切线的性质、圆周角定理、相似三角形的性质和判定,掌握此类问题的辅助线的作法是解题的关键.

练习册系列答案
相关题目
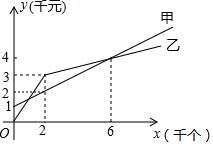 某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费,甲乙两厂所收取的费用y(千元)与证书数量x(千个)的函数关系图象分别如图中甲、乙所示.
某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费,甲乙两厂所收取的费用y(千元)与证书数量x(千个)的函数关系图象分别如图中甲、乙所示. 如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1),规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次交换,如此这样,连续经过2016次变换后,正方形ABCD的对角线交点M的坐标变为(-2014,2).
如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1),规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次交换,如此这样,连续经过2016次变换后,正方形ABCD的对角线交点M的坐标变为(-2014,2). 如图,四边形ABCD是平行四边形,且AB=AC,过A,B,C三点的⊙O与DC的延长线交于点E,连接AE交BC于F.
如图,四边形ABCD是平行四边形,且AB=AC,过A,B,C三点的⊙O与DC的延长线交于点E,连接AE交BC于F.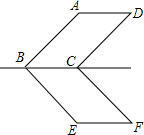 如图,?ABCD与?EBCF关于BC所在直线对称,∠ABE=90°,求∠F.
如图,?ABCD与?EBCF关于BC所在直线对称,∠ABE=90°,求∠F.