题目内容
4.(1)计算:$\root{3}{-8}-{(\frac{1}{2})^{-1}}+|{\sqrt{3}-2}|+tan{60°}$;(2)解方程组:$\left\{\begin{array}{l}{3(x-1)=5y+1}\\{x=2y}\end{array}$.
分析 (1)原式第一项利用立方根定义计算,第二项利用负整数指数幂法则计算,第三项利用绝对值的代数意义化简,最后一项利用特殊角的三角函数值计算即可得到结果;
(2)方程组整理后,利用代入消元法求出解即可.
解答 解:(1)原式=-2-2+2-$\sqrt{3}$+$\sqrt{3}$=-2;
(2)方程组整理得:$\left\{\begin{array}{l}{3x-5y=4①}\\{x=2y②}\end{array}\right.$,
把②代入①得:6y-5y=4,即y=4,
把y=4代入②得:x=8,
则方程组的解为$\left\{\begin{array}{l}{x=8}\\{y=4}\end{array}\right.$.
点评 此题考查了实数的运算,以及解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
19.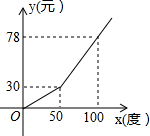 某地电力公司的用电收费标准如图,x(度)表示用户每月的用电量,y(元)表示每月应付的电费,看图可知,当用户一个月的用电量超过50度时,超过部分的收费标准是每度( )
某地电力公司的用电收费标准如图,x(度)表示用户每月的用电量,y(元)表示每月应付的电费,看图可知,当用户一个月的用电量超过50度时,超过部分的收费标准是每度( )
 某地电力公司的用电收费标准如图,x(度)表示用户每月的用电量,y(元)表示每月应付的电费,看图可知,当用户一个月的用电量超过50度时,超过部分的收费标准是每度( )
某地电力公司的用电收费标准如图,x(度)表示用户每月的用电量,y(元)表示每月应付的电费,看图可知,当用户一个月的用电量超过50度时,超过部分的收费标准是每度( )| A. | 0.96元 | B. | 0.78元 | C. | 0.60元 | D. | 0.3元 |
9.要使分式$\frac{x+2}{x-1}$有意义,则x的取值应满足( )
| A. | x≠-2 | B. | x≠1 | C. | x=-2 | D. | x=1 |
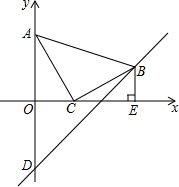 在平面直角坐标系中,现将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,且点A(0,2),点C(1,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D.
在平面直角坐标系中,现将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,且点A(0,2),点C(1,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D. 如图,在△ABC中,∠B=60°,AD平分∠BAC交BC于D,若AB+BD=AC,那么∠C=30度.
如图,在△ABC中,∠B=60°,AD平分∠BAC交BC于D,若AB+BD=AC,那么∠C=30度.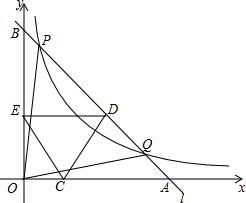 如图,已知双曲线y=$\frac{k}{x}(x>0)$与经过点A(1,0),B(0,1)的直线交于P,Q两点,且P的横坐标与Q的纵坐标都是$\frac{1}{4}$,连接OP,OQ.
如图,已知双曲线y=$\frac{k}{x}(x>0)$与经过点A(1,0),B(0,1)的直线交于P,Q两点,且P的横坐标与Q的纵坐标都是$\frac{1}{4}$,连接OP,OQ.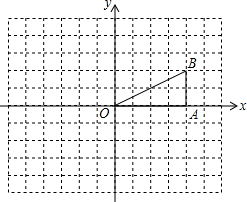 如图,在△OAB中,∠OAB=90°,且点B的坐标为(4,2).
如图,在△OAB中,∠OAB=90°,且点B的坐标为(4,2).