题目内容
14.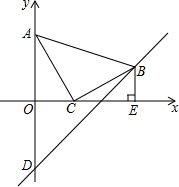 在平面直角坐标系中,现将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,且点A(0,2),点C(1,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D.
在平面直角坐标系中,现将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,且点A(0,2),点C(1,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D.(1)求证:△AOC≌△CEB;
(2)求△ABD的面积.
分析 (1)根据等腰直角三角形的性质,可得AC=BC,∠ACB=90°,根据余角的性质,可得∠OAC=∠BCE,根据AAS,可得答案;
(2)根据全等三角形的性质,可得B点坐标,根据待定系数法,可得b的值,根据三角形的面积公式,可得答案.
解答 (1)证明:∵BE⊥CE,
∴∠BEC=90°,
∵△ABC是等腰直角三角形,
∴AC=BC,∠ACB=90°.
∵∠O=∠ACB=90°,
∴∠OAC+∠ACO=90°,∠ACO+∠BCE=90°,
∴∠OAC=∠BCE.
在RtAOC和Rt△CEB中,
$\left\{\begin{array}{l}{∠O=∠CEB}\\{∠OAC=∠CEB}\\{AC=CB}\end{array}\right.$,
∴RtAOC≌Rt△CEB (AAS);
(2)如图:作BF⊥y轴于F点.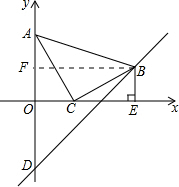
∵RtAOC≌Rt△CEB,
∴CE=OA=2,BE=OC=1,
∴OE=CC+CE=1+2=3,
即B(3,1),BF=3.
将B点坐标代入y=x+b,得
3+b=1,
解得b=-2,
直线BD的解析式为y=x-2,
当x=0时,y=-2,即D(0,-2).
S△ABD=$\frac{1}{2}$AD•BF=$\frac{1}{2}$×[2-(-2)]×3=6.
点评 本题考查了一次函数综合题,(1)利用余角的性质得出∠OAC=∠BCE是解题关键;(2)利用待定系数法求出b值,又利用了三角形的面积公式.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目

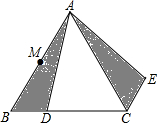 如图,△ABC是等边三角形,D是BC上一点,△ABD经过逆时针旋转后到达△ACE的位置.
如图,△ABC是等边三角形,D是BC上一点,△ABD经过逆时针旋转后到达△ACE的位置.