题目内容
7.如图,转盘上1、2、3、4四个数字分别代表鸡、猴、鼠、羊四种生肖邮票(每种邮票各两枚,鸡年邮票面值“80分”,其它邮票都是面值“1.20元”),转动转盘后,指针每落在某个数字所在扇形一次就表示获得该种邮票一枚.(1)任意转动转盘一次,获得猴年邮票的概率是$\frac{1}{4}$;
(2)任意转动转盘两次,求获得的两枚邮票可以邮寄一封需2.4元邮资的信件的概率.

分析 (1)根据题意可以求得任意转动转盘一次,获得猴年邮票的概率;
(2)根据题意可以写出转动转盘两次,所有可能出现的结果,然后找出符合要求的可能结果,即可求得相应的概率.
解答 解:(1)由题意可得,
任意转动转盘一次,获得猴年邮票的概率是$\frac{1}{4}$,
故答案为:$\frac{1}{4}$;
(2)∵转动转盘两次,所有可能出现的结果有:(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共有16种,它们出现的可能性相同,
∴所有的结果中,满足“转动转盘两次,获得的两枚邮票可以邮寄一封需2.4元邮资的信件”(记为事件A)的结果有9种,所以P(A)=$\frac{9}{16}$,
即任意转动转盘两次,获得的两枚邮票可以邮寄一封需2.4元邮资的信件的概率是$\frac{9}{16}$.
点评 本题考查列表法与树状图法,解题的关键是明确题意,可以算出相应事件发生的可能性和发生的所有可能性,会计算相应的事件的概率.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
11.若x1,x2是x2-x-3=0的两个实数根,则-x1-x2=( )
| A. | ±1 | B. | -3 | C. | -1 | D. | 3 |
15.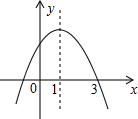 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:
①abc>0;②b2-4ac<0;③2a+b=0;④a+b>0.
则其中正确结论的个数是( )
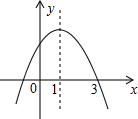 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:①abc>0;②b2-4ac<0;③2a+b=0;④a+b>0.
则其中正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.地球的表面积约为511000000km2,511000000用科学记数法表示正确的是( )
| A. | 0.511×109 | B. | 5.11×108 | C. | 51.1×107 | D. | 511×106 |
 如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点B逆时针旋转60°得到△A′BC′,连接A′C,则A′C的长为4+3$\sqrt{3}$.
如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点B逆时针旋转60°得到△A′BC′,连接A′C,则A′C的长为4+3$\sqrt{3}$. 如图,在△ABC和△DCB中,AB=DC,AC=DB,AC与DB交于点M.
如图,在△ABC和△DCB中,AB=DC,AC=DB,AC与DB交于点M.