题目内容
18. 如图,AB为⊙O的直径,弦CD⊥AB于H,E为AB延长线上一点,CE交⊙O于点F
如图,AB为⊙O的直径,弦CD⊥AB于H,E为AB延长线上一点,CE交⊙O于点F(1)求证:BF平分∠DFE;
(2)若EF=DF,BE=5,AH=$\frac{9}{4}$,求⊙O的半径.
分析 (1)根据圆内接四边形性质和圆周角定理求出∠EFB=∠CDB,∠BCD=∠DFB,根据垂径定理求出CH=DH,求出BC=BD,根据等腰三角形性质求出∠BCD=∠CDB,求出∠EFB=∠DFB即可;
(2)根据全等三角形的判定求出△DFB≌△EFB,根据全等三角形的性质求出BD=BE=5,证△DHB∽△ADB,根据相似得出比例式,代入求出即可.
解答 (1)证明:∵C、D、B、F四点共圆,
∴∠EFB=∠CDB,∠BCD=∠DFB,
∵CD⊥OA,OA过O,
∴CH=DH,
∴BC=BD,
∴∠BCD=∠CDB,
∴∠EFB=∠DFB,
∴BF平分∠DFE;
(2)解:设⊙O的半径为R,
∵在△DFB和△EFB中
$\left\{\begin{array}{l}{DF=EF}\\{∠DFB=∠EFB}\\{FB=FB}\end{array}\right.$
∴△DFB≌△EFB(SAS),
∴BD=BE,
∵BE=5,
∴BD=5,
∵AB为⊙O直径,CD⊥AB,
∴∠ADB=∠DHB=90°,
∵∠DBH=∠ABD,
∴△DHB∽△ADB,
∴$\frac{BD}{AB}$=$\frac{BH}{BD}$,
∵AH=$\frac{9}{4}$,BD=5,AB=2R,BH=2R-$\frac{9}{4}$,
∴$\frac{5}{2R}$=$\frac{2R-\frac{9}{4}}{5}$,
解得:R=$\frac{25}{8}$,R=-2(舍去),
即⊙O的半径是$\frac{25}{8}$.
点评 本题考查了圆周角定理,相似三角形的性质和判定,圆内接四边形,垂径定理等知识点,能综合运用定理进行推理是解此题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
8.下面的说法正确的是( )
| A. | -2不是单项式 | B. | -a表示负数 | C. | $\frac{3ab}{5}$的系数是3 | D. | x2+2x+1是多项式 |
6.用科学记数法表示数2350为( )
| A. | 2.350×103 | B. | 0.2350×104 | C. | 0.2350×103 | D. | 2.350×104 |
1.下列判断错误的是( )
| A. | 当a≠0时,分式$\frac{2}{a}$有意义 | B. | 当a=-3时,分式$\frac{a+3}{{{a^2}-9}}$有意义 | ||
| C. | 当$a=-\frac{1}{2}$时,分式$\frac{2a+1}{a}$的值为0 | D. | 当a=1时,分式$\frac{2a-1}{a}$的值为1 |
 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为55°.
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为55°.
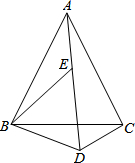 如图,已知△ABC和△BDE均为等边三角形,求证:BD+CD=AD.
如图,已知△ABC和△BDE均为等边三角形,求证:BD+CD=AD. 等腰△ABC、△EFC中,AB=AC,FE=FC,D为BE的中点,∠BAC+∠EFC=180°,求证:AD⊥FD.
等腰△ABC、△EFC中,AB=AC,FE=FC,D为BE的中点,∠BAC+∠EFC=180°,求证:AD⊥FD.