题目内容
3.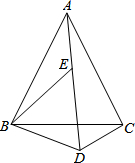 如图,已知△ABC和△BDE均为等边三角形,求证:BD+CD=AD.
如图,已知△ABC和△BDE均为等边三角形,求证:BD+CD=AD.
分析 首先证明△ABE≌△CBD,进而得到DC=AE,再由AD=AE+ED利用等量代换AD=BD+CD.
解答 证明:∵△ABC和△BDE都是等边三角形,
∴AB=AC,EB=DB=ED,∠ABC=∠EBD=60°,
∴∠ABC-∠EBC=∠EBD-∠EBC,
即∠ABE=∠CBD,
在△ABE和△CBD中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠CBD}\\{BD=BE}\end{array}\right.$,
∴△ABE≌△CBD(SAS),
∴DC=AE,
∵AD=AE+ED,
∴AD=BD+CD.
点评 此题主要考查了全等三角形的判定与性质,关键是掌握全等三角形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.不等式4x-k≤0的正整数解是1,2,3,那么k的取值范围是( )
| A. | 12≤k<16 | B. | 12<k<16 | C. | 3≤k<4 | D. | 3<k≤4 |
 如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.
如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD. 如图,AB为⊙O的直径,弦CD⊥AB于H,E为AB延长线上一点,CE交⊙O于点F
如图,AB为⊙O的直径,弦CD⊥AB于H,E为AB延长线上一点,CE交⊙O于点F
 如图所示的几何体是由9个小正方体组合而成的,它的左视图是( )
如图所示的几何体是由9个小正方体组合而成的,它的左视图是( )



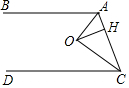 如图,AB∥CD,OA,OC分别平分∠BAC和∠ACD,OH⊥AC于点H,且OH=4,则AB,CD之间的距离为8.
如图,AB∥CD,OA,OC分别平分∠BAC和∠ACD,OH⊥AC于点H,且OH=4,则AB,CD之间的距离为8.