Question

7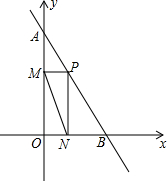．已知直线AB与y轴交于点A（0，10），与x轴交于点B（5，0）．
（1）求直线AB的解析式；
（2）在平面内确定点C，使得以点O，A，B，C为顶点的四边形是平行四边形，请直接写出点C的坐标；
（3）如图，若点P为线段AB上的一个动点，作PM⊥y轴于点M，作PN⊥x轴于点N，连接MN，问是否存在点P，使MN的值最小？若存在，求出此时MN的值．

Answer 1

分析 （1）利用待定系数法求解即可；
（2）分三种情况）①过点A作x轴的平行线，过点O作AB的平行线，交于点C，组成的平行四边形，②过点B作y轴的平行线，过点O作AB的平行线，交于点C，组成的平行四边形，③过点A作x轴的平行线，过点B作y轴的平行线，交于点C，组成的平行四边形；
（3）连接OP，易得四边形ONPM是矩形，可得OP=MN，在RT△AOB中，当OP⊥AB时，OP最短，即MN最小，利用三角形的面积可得OP的值，即当点P运动到使OP⊥AB于点P时，MN最小，最小值为2$\sqrt{5}$．

解答 解：（1）设直线AB的函数解析式为y=kx+b，
∵过点A（0，10），点B（5，0）．
∴$\left\{\begin{array}{l}{5k+b=0}\\{b=10}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=-2}\\{b=10}\end{array}\right.$．
∴直线AB的函数解析式为y=-2x+10，
（2）①如图1，过点A作x轴的平行线，过点O作AB的平行线，交于点C，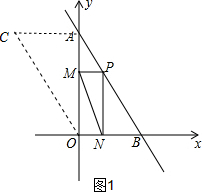

∵AC∥x轴，OC∥AB，
∴四边形OABC为平行四边形，
∴C（-5，10），
②如图2，过点B作y轴的平行线，过点O作AB的平行线，交于点C，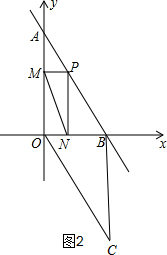

∵BC∥y轴，OC∥AB，
∴四边形OABC为平行四边形，
∴C（5，-10），
③如图3，过点A作x轴的平行线，过点B作y轴的平行线，交于点C，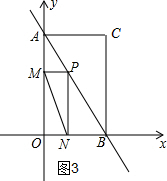

∵AC∥OB，BC∥AO，
∴四边形OABC为平行四边形，
∴C（5，10），
综上所述，点C的坐标为（-5，10），（5，-10）或C（5，10）；
（3）存在点P，使MN的值最小．
如图4，连接OP，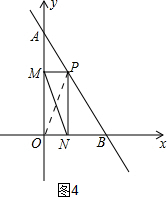

由已知可得∠PMO=∠MON=∠ONP=90°，
∵四边形ONPM是矩形，
∴OP=MN，
在RT△AOB中，当OP⊥AB时，OP最短，即MN最小，
∵A（0，10），B（5，0），
∴AO=10，BO=5，
∴AB=$\sqrt{1{0}^{2}+{5}^{2}}$=5$\sqrt{5}$，
∵S_△AOB=$\frac{1}{2}$AO•BO=$\frac{1}{2}$AB•OP，
∴OP=2$\sqrt{5}$，
∴MN=2$\sqrt{5}$，即当点P运动到使OP⊥AB于点P时，MN最小，最小值为2$\sqrt{5}$．

点评 本题主要考查了一次函数综合题，涉及勾股定理，矩形的性质，一次函数解析式等知识，解题的关键是分三种情况作出图形，求出点C的坐标．