题目内容
18．不等式组$\left\{\begin{array}{l}{2-x＞-2x}\\{-5+3x＜x+3}\end{array}\right.$的解集是-2＜x＜4．分析 先求出每个不等式的解集，再求出不等式组的解集即可．
解答 解：$\left\{\begin{array}{l}{2-x＞-2x①}\\{-5+3x＜x+3②}\end{array}\right.$
∵∵解不等式①得：x＞-2，
解不等式②得：x＜4，
∴不等式组的解集为-2＜x＜4，
故答案为：-2＜x＜4．
点评 本题考查了解一元一次不等式组的应用，解此题的关键是能根据不等式的解集求出不等式组的解集．
练习册系列答案
相关题目
8．若二次根式$\sqrt{3x-2}$在实数范围内有意义，则x的取值范围是（ ）
| A． | x＜$\frac{2}{3}$ | B． | x≤$\frac{2}{3}$ | C． | x＞$\frac{2}{3}$ | D． | x≥$\frac{2}{3}$ |
已知AB∥DE，∠B=60°，且CM平分∠DCB，CM⊥CN，垂足为C，求∠NCE的度数．
如图，已知函数y=2x和函数y=$\frac{k}{x}$的图象交于A、B两点，过点A作AE⊥x轴于点E，若△AOE的面积为4，P是坐标平面上的点，且以点B、O、E、P为顶点的四边形是平行四边形，则k=8，满足条件的P点坐标是（0，-4）或（-4，-4）或（4，4）．
13．向阳村2010年的人均年收入为12000元，2012年的人均年收入为14520元．设人均年收入的平均增长率为x，则下列所列的方程中正确的是（ ）
| A． | 14520（1-x2）=12000 | B． | 12000（1+x）2=14520 | C． | 12000（1+x）2=14520 | D． | 12000（1-x）2=14520 |
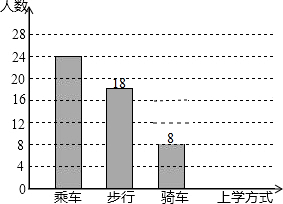某校为了进行交通安全教育，对九年一班n名学生上学方式：乘车、步行、骑自行车情况进行了调查，并根据调查结果绘制成如图所示的条形统计图．
10．下列运算中，正确的是（ ）
| A． | x3•x2=x6 | B． | 2x3÷x2=2x | C． | x+x2=x3 | D． | （$\frac{x}{2}$）3=$\frac{{x}^{3}}{2}$ |
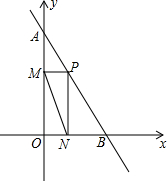已知直线AB与y轴交于点A（0，10），与x轴交于点B（5，0）．