题目内容
4.对于二次函数y=-x2+2x.有下列四个结论:①它的对称轴是直线x=1;②y随x的增大而增大;③它的图象与x轴的两个交点是(0,0)和(2,0);④当0<x<2时,y>0.其中正确的结论的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用配方法求出二次函数对称轴,再求出图象与x轴交点坐标,进而结合二次函数性质得出答案.
解答 解:y=-x2+2x=-(x-1)2+1,故①它的对称轴是直线x=1,正确;
②∵a=-1<0,∴开口向下,当x<1时y随着x的增大而增大,错误;
③当y=0,则x(-x+2)=0,解得:x1=0,x2=2,
故它的图象与x轴的两个交点是(0,0)和(2,0),正确;
④∵a=-1<0,
∴抛物线开口向下,
∵它的图象与x轴的两个交点是(0,0)和(2,0),
∴当0<x<2时,y>0,正确.
故选C.
点评 本题主要考查了二次函数的性质以及一元二次方程的解法,得出抛物线的对称轴和其交点坐标是解题关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
15.练习中,小明同学做了如下4道因式分解题,你认为小明做得正确的有( )
①x3+x=x(x+1)(x-1);
②x2-2xy+y2=(x-y)2;
③a2-a+1=a(a-1)+1;
④x2-16y2=(x+4y)(x-4y).
①x3+x=x(x+1)(x-1);
②x2-2xy+y2=(x-y)2;
③a2-a+1=a(a-1)+1;
④x2-16y2=(x+4y)(x-4y).
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.如果a>b,则下列不等式中成立的是( )
| A. | a-3<b-3 | B. | 3-a<3-b | C. | $\frac{1}{3}$a<$\frac{1}{3}$b | D. | -2a>-2b |
14. 如图,AD是△ABC的中线,E是AD中点,BE的延长线与AC交于点F,则AF:AC等于( )
如图,AD是△ABC的中线,E是AD中点,BE的延长线与AC交于点F,则AF:AC等于( )
 如图,AD是△ABC的中线,E是AD中点,BE的延长线与AC交于点F,则AF:AC等于( )
如图,AD是△ABC的中线,E是AD中点,BE的延长线与AC交于点F,则AF:AC等于( )| A. | 1:2 | B. | 2:3 | C. | 1:3 | D. | 2:5 |
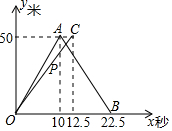 甲、乙两人在相邻两条直跑道上进行竞走比赛(注:跑道长50米,两人均往返一次,返回时转身的时间忽略不计),图中的折线OA-AB是甲离出发点的距离y(米)与比赛时间x(秒)的函数图象;线段OC是乙离出发点的距离y(米)与比赛时间x(秒)的函数图象,其中x≥0,线段OC与AB相交于点P.根据图象,解决下列问题:
甲、乙两人在相邻两条直跑道上进行竞走比赛(注:跑道长50米,两人均往返一次,返回时转身的时间忽略不计),图中的折线OA-AB是甲离出发点的距离y(米)与比赛时间x(秒)的函数图象;线段OC是乙离出发点的距离y(米)与比赛时间x(秒)的函数图象,其中x≥0,线段OC与AB相交于点P.根据图象,解决下列问题: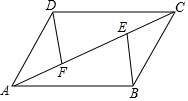 如图,E,F是四边形ABCD的对角线AC上点,AF=CE,DF=BE,DF∥BE.
如图,E,F是四边形ABCD的对角线AC上点,AF=CE,DF=BE,DF∥BE.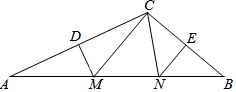 如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N,
如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N,