题目内容
19.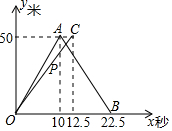 甲、乙两人在相邻两条直跑道上进行竞走比赛(注:跑道长50米,两人均往返一次,返回时转身的时间忽略不计),图中的折线OA-AB是甲离出发点的距离y(米)与比赛时间x(秒)的函数图象;线段OC是乙离出发点的距离y(米)与比赛时间x(秒)的函数图象,其中x≥0,线段OC与AB相交于点P.根据图象,解决下列问题:
甲、乙两人在相邻两条直跑道上进行竞走比赛(注:跑道长50米,两人均往返一次,返回时转身的时间忽略不计),图中的折线OA-AB是甲离出发点的距离y(米)与比赛时间x(秒)的函数图象;线段OC是乙离出发点的距离y(米)与比赛时间x(秒)的函数图象,其中x≥0,线段OC与AB相交于点P.根据图象,解决下列问题:(1)求线段OC,AB对应的函数关系式,并写出相应的自变量x的取值范围;
(2)直接写出点P的坐标,并说明点P的横、纵坐标的实际意义;
(3)若乙往返时的速度相等且均为匀速运动,请在图中画出乙返回时的图象,并标明乙返回出发点的时间.
分析 (1)根据图象中数据可以分别求得线段OC,AB对应的函数关系式,并写出相应的自变量x的取值范围;
(2)根据(1)中的函数解析式可以求得点P的坐标,并写出点P的横、纵坐标的实际意义;
(3)根据题意可以直接画出相应的函数图象,本题得以解决.
解答 解:(1)设线段OC对应的函数解析式为y=kx,
12.5k=50,
解得,k=4,
∴线段OC对应的函数解析式为y=4x(0≤x≤12.5),
设线段AB对应的函数解析式为y=ax+b,
则$\left\{\begin{array}{l}{10a+b=50}\\{22.5a+b=0}\end{array}\right.$,得$\left\{\begin{array}{l}{a=-4}\\{b=90}\end{array}\right.$,
∴线段AB对应的函数解析式为y=-4x+90(10≤x≤22.5);
(2)由题意可得,
4x=-4x+90,得x=11.25,
∴y=4x=4×11.25=45,
即点P的坐标为(11.25,45),
点P的横、纵坐标的实际意义是在出发11.25秒时,甲乙相遇,相遇点距出发点45米;
(3)如下图所示,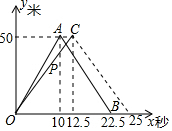 .
.
点评 本题考查一次函数的应用,解答此类问题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
相关题目
10.下列根式中不是最简二次根式的是( )
| A. | $\sqrt{13}$ | B. | $\sqrt{12}$ | C. | $\sqrt{{a}^{2}+4}$ | D. | $\sqrt{2}$ |
4.对于二次函数y=-x2+2x.有下列四个结论:①它的对称轴是直线x=1;②y随x的增大而增大;③它的图象与x轴的两个交点是(0,0)和(2,0);④当0<x<2时,y>0.其中正确的结论的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
11.下列结论正确的是( )
| A. | 近似数1.230和1.23表示的意义相同 | |
| B. | 近似数79.0是精确到个位的数 | |
| C. | 将数60340精确到千位是6.0×104 | |
| D. | 近似数5千与近似数5000的精确度相同 |
8.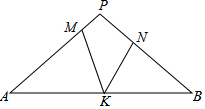 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=42°,则∠P的度数为( )
如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=42°,则∠P的度数为( )
 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=42°,则∠P的度数为( )
如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=42°,则∠P的度数为( )| A. | 44° | B. | 66° | C. | 96° | D. | 92° |
9.已知cosα=0.8391,cotβ=0.5774,则锐角α,β的大小关系是( )
| A. | α>β | B. | α≤β | C. | α<β | D. | α=β |

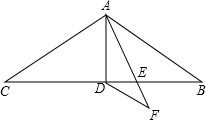 如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为( )
如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为( ) 一位旅行者在早晨8时从城市出发到乡村,第一个小时走了5千米,然后他上坡,1个小时只走了3千米,以后就休息;休息后平均每小时走4千米,在中午12时到达乡村.根据下图回答问题:
一位旅行者在早晨8时从城市出发到乡村,第一个小时走了5千米,然后他上坡,1个小时只走了3千米,以后就休息;休息后平均每小时走4千米,在中午12时到达乡村.根据下图回答问题: