题目内容
12.先化简再求值:$\sqrt{{a}^{2}+\frac{1}{{a}^{2}}-2}$+$\sqrt{{a}^{2}+\frac{1}{{a}^{2}}+2}$.其中a=$\sqrt{3}$-1.分析 根据完全平方公式和算术平方根可以化简题目中的式子,然后将a的值代入即可解答本题.
解答 解:$\sqrt{{a}^{2}+\frac{1}{{a}^{2}}-2}$+$\sqrt{{a}^{2}+\frac{1}{{a}^{2}}+2}$
=$\sqrt{(a-\frac{1}{a})^{2}}+\sqrt{(a+\frac{1}{a})^{2}}$
∵a=$\sqrt{3}$-1,
∴$\frac{1}{a}=\frac{\sqrt{3}+1}{2}$,
∴a-$\frac{1}{a}$=$\sqrt{3}-1-\frac{\sqrt{3}+1}{2}=\frac{\sqrt{3}-3}{2}$<0,a+$\frac{1}{a}=\sqrt{3}-1+\frac{\sqrt{3}+1}{2}$=$\frac{3\sqrt{3}-1}{2}$>0,
∴原式=$\frac{1}{a}-a+a+\frac{1}{a}$=$\frac{2}{a}$=$2×\frac{\sqrt{3}+1}{2}$=$\sqrt{3}$+1.
点评 本题考查二次根式的化简求值,解答本题的关键是明确二次根式化简求值的方法.

练习册系列答案
相关题目
1.不在一次函数y=2x+4的图象上的点是( )
| A. | (1,6) | B. | (0,4) | C. | (2,3) | D. | (-2,0) |
 如图,已知正比例函数与反比例函数的图象在第一象限的交点为A(2,4).
如图,已知正比例函数与反比例函数的图象在第一象限的交点为A(2,4).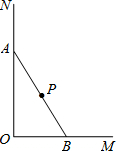 如图,木杆AB斜靠在墙壁上,∠OAB=30°,AB=4米.当木杆的上端A沿墙壁NO下滑时,木杆的底端B也随之沿着地面上的射线OM方向滑动.设木杆的顶端A匀速下滑到点O停止,则木杆的中点P到射线OM的距离y(米)与下滑的时间x(秒)之间的函数图象大致是( )
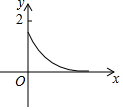
如图,木杆AB斜靠在墙壁上,∠OAB=30°,AB=4米.当木杆的上端A沿墙壁NO下滑时,木杆的底端B也随之沿着地面上的射线OM方向滑动.设木杆的顶端A匀速下滑到点O停止,则木杆的中点P到射线OM的距离y(米)与下滑的时间x(秒)之间的函数图象大致是( )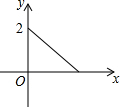
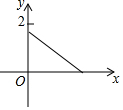

 “奔跑吧,兄弟!”节目组预设计一个新游戏:“奔跑”路线A、B、C、D四地,如图A、B、C三地在同一直线上,D在A北偏东30°方向,在C北偏西45°方向,C在A北偏东75°方向,且BD=BC=40m,从A地到D地的距离是20$\sqrt{6}$m.
“奔跑吧,兄弟!”节目组预设计一个新游戏:“奔跑”路线A、B、C、D四地,如图A、B、C三地在同一直线上,D在A北偏东30°方向,在C北偏西45°方向,C在A北偏东75°方向,且BD=BC=40m,从A地到D地的距离是20$\sqrt{6}$m.