题目内容
4. “奔跑吧,兄弟!”节目组预设计一个新游戏:“奔跑”路线A、B、C、D四地,如图A、B、C三地在同一直线上,D在A北偏东30°方向,在C北偏西45°方向,C在A北偏东75°方向,且BD=BC=40m,从A地到D地的距离是20$\sqrt{6}$m.
“奔跑吧,兄弟!”节目组预设计一个新游戏:“奔跑”路线A、B、C、D四地,如图A、B、C三地在同一直线上,D在A北偏东30°方向,在C北偏西45°方向,C在A北偏东75°方向,且BD=BC=40m,从A地到D地的距离是20$\sqrt{6}$m.
分析 过点D作DE⊥BC于E,由方向角可得出∠DAC=45°、∠BCD=60°,结合BC=BD=40m,即可得出△BCD为等边三角形,进而可得出DE的长度,在Rt△ADE中,由∠AED=90°、∠DAE=45°,可得出AE=DE=20$\sqrt{3}$m,再利用勾股定理即可得出AD的长度.
解答 解:过点D作DE⊥BC于E,如图所示.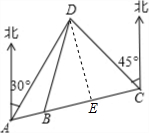
由题意可知:∠DAC=75°-30°=45°,∠BCD=180°-75°-45°=60°.
∵BC=BD=40m,
∴△BCD为等边三角形,
∴DE=$\frac{\sqrt{3}}{2}$BD=20$\sqrt{3}$m.
在Rt△ADE中,∠AED=90°,∠DAE=45°,
∴∠ADE=45°,
∴AE=DE=20$\sqrt{3}$m,AD=$\sqrt{A{E}^{2}+D{E}^{2}}$=20$\sqrt{6}$m.
故答案为:20$\sqrt{6}$.
点评 本题考查了解直角三角形的应用中的方向角问题、勾股定理的应用以及等边三角形的判定与性质,根据方向角结合BC=BD找出△BCD为等边三角形是解题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
14.在0.1,3,$\sqrt{2}$和$\frac{1}{3}$这四个实数中,无理数是( )
| A. | 0.1 | B. | 3 | C. | $\sqrt{2}$ | D. | $\frac{1}{3}$ |
19.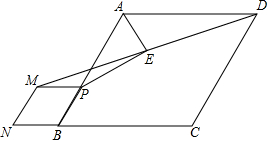 如图,在菱形ABCD中,tan∠ABC=$\frac{4}{3}$,P为AB上一点,以PB为边向外作菱形PMNB,连结DM,取DM中点E,连结AE,PE,则$\frac{AE}{PE}$的值为( )
如图,在菱形ABCD中,tan∠ABC=$\frac{4}{3}$,P为AB上一点,以PB为边向外作菱形PMNB,连结DM,取DM中点E,连结AE,PE,则$\frac{AE}{PE}$的值为( )
 如图,在菱形ABCD中,tan∠ABC=$\frac{4}{3}$,P为AB上一点,以PB为边向外作菱形PMNB,连结DM,取DM中点E,连结AE,PE,则$\frac{AE}{PE}$的值为( )
如图,在菱形ABCD中,tan∠ABC=$\frac{4}{3}$,P为AB上一点,以PB为边向外作菱形PMNB,连结DM,取DM中点E,连结AE,PE,则$\frac{AE}{PE}$的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
 如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段BN的长度,这样测量的依据是垂线段最短.
如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段BN的长度,这样测量的依据是垂线段最短.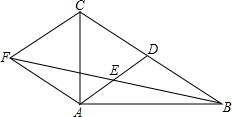 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.