题目内容
20.解不等式组$\left\{\begin{array}{l}{5x-1>3(x+1)}\\{\frac{x-2}{2}≤7-\frac{3x}{2}}\end{array}\right.$并把它的解集在数轴上表示出来.分析 根据解不等式组的方法可以求得原不等式组的解集,并且在数轴上可以表示出来.
解答 解:$\left\{\begin{array}{l}{5x-1>3(x+1)}&{①}\\{\frac{x-2}{2}≤7-\frac{3x}{2}}&{②}\end{array}\right.$,
由不等式①,得
x>2,
由不等式②,得
x≤4,
由不等式①②可得,原不等式组的解集是:2<x≤4,在数轴上表示如下图所示, .
.
点评 本题考查解一元一次不等式组、在数轴上表示不等式组的解集,解答本题的关键是明确解一元一次不等式组的方法.

练习册系列答案
相关题目
8.下列计算①(-1)0=-1;②(-1)-1=-1;③2×2-2=$\frac{1}{2}$;④3a-2=$\frac{1}{{3a}^{2}}$;⑤(-a2)m=(-am)2.正确的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
10.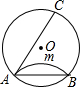 如图,将⊙O沿弦AB折叠得到$\widehat{AmB}$所在圆的切线交⊙O于点C,若⊙O的半径为1,当AC取最大值时,则弦AB的长是( )
如图,将⊙O沿弦AB折叠得到$\widehat{AmB}$所在圆的切线交⊙O于点C,若⊙O的半径为1,当AC取最大值时,则弦AB的长是( )
 如图,将⊙O沿弦AB折叠得到$\widehat{AmB}$所在圆的切线交⊙O于点C,若⊙O的半径为1,当AC取最大值时,则弦AB的长是( )
如图,将⊙O沿弦AB折叠得到$\widehat{AmB}$所在圆的切线交⊙O于点C,若⊙O的半径为1,当AC取最大值时,则弦AB的长是( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
 如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段BN的长度,这样测量的依据是垂线段最短.
如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段BN的长度,这样测量的依据是垂线段最短.