题目内容
2.解下列方程:(1)$\frac{3}{x}$=$\frac{2}{x+1}$
(2)$\frac{x-8}{x-7}$=8+$\frac{1}{7-x}$.
分析 根据等式的性质,可转化成整式方程,根据解方程,可得答案.
解答 解:(1)方程两边都乘以x(x+1),得
3(x+1)=2x,
解得x=-3,
检验:x=-3时,x(x+3)≠0,
∴x=-3是原分式方程的解;
(2)方程两边都乘以(x-7),得
x-8=8(x-7)-1,
解得x=7,
检验:x=7时x-7=0,
∴x=7是方程的增根,
∴原方程无解.
点评 本题考查了解分式方程,利用等式的性质把分式方程转化成整式方程是解题关键.

练习册系列答案
相关题目
10.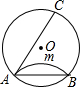 如图,将⊙O沿弦AB折叠得到$\widehat{AmB}$所在圆的切线交⊙O于点C,若⊙O的半径为1,当AC取最大值时,则弦AB的长是( )
如图,将⊙O沿弦AB折叠得到$\widehat{AmB}$所在圆的切线交⊙O于点C,若⊙O的半径为1,当AC取最大值时,则弦AB的长是( )
 如图,将⊙O沿弦AB折叠得到$\widehat{AmB}$所在圆的切线交⊙O于点C,若⊙O的半径为1,当AC取最大值时,则弦AB的长是( )
如图,将⊙O沿弦AB折叠得到$\widehat{AmB}$所在圆的切线交⊙O于点C,若⊙O的半径为1,当AC取最大值时,则弦AB的长是( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
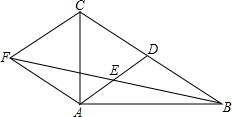 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.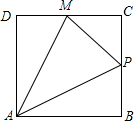 如图,在边长为1的正方形ABCD的边上有一点P按A→B→C→M的顺序运动,M是边CD上的中点,设点P经过的路程x为自变量,△APM的面积为y,则函数的大致图象是( )
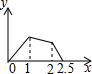
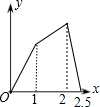
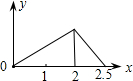
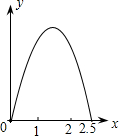
如图,在边长为1的正方形ABCD的边上有一点P按A→B→C→M的顺序运动,M是边CD上的中点,设点P经过的路程x为自变量,△APM的面积为y,则函数的大致图象是( )