题目内容
18.函数的自变量x满足$\frac{1}{2}$≤x≤2时,函数值y满足$\frac{1}{4}$≤y≤1,则这个函数表达式可以是y=-$\frac{1}{2}$x+2(答案不唯一).(只需写出一个即可)分析 设该函数的解析式为y=kx+b(k≠0),再把x=$\frac{1}{2}$,y=$\frac{1}{4}$;x=2,y=1代入求出k、b的值即可.
解答 解:设该函数的解析式为y=kx+b(k≠0),
∵x=$\frac{1}{2}$,y=$\frac{1}{4}$;x=2,y=1,
∴$\left\{\begin{array}{l}\frac{1}{2}k+b=\frac{1}{4}\\ 2k+b=1\end{array}\right.$,解得$\left\{\begin{array}{l}k=-\frac{1}{2}\\ b=2\end{array}\right.$,
∴这个函数表达式可以是y=-$\frac{1}{2}$x+2.
故答案为:y=-$\frac{1}{2}$x+2(答案不唯一).
点评 本题考查的是一次函数的性质,根据x、y的取值范围得出其对应值,利用待定系数法求出一次函数的解析式是解题的关键,此题属开放性题目,答案不唯一.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
6.下列方程中有两个相等实数根的是( )
| A. | 2x2+4x+35=0 | B. | x2+1=2x | C. | (x-1)2=-1 | D. | 5x2+4x=1 |
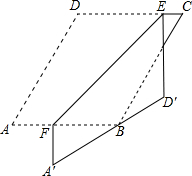 如图,在?ABCD纸片中,∠A=60°,AD-AB=1,点E,F分别在边CD,AB上,将纸片沿EF折叠,使点A,D分别落在点A′,D′,处,且AD经过点B.当D′E⊥CD时,CE=1,则AB的长是$\frac{3\sqrt{3}+5}{2}$.
如图,在?ABCD纸片中,∠A=60°,AD-AB=1,点E,F分别在边CD,AB上,将纸片沿EF折叠,使点A,D分别落在点A′,D′,处,且AD经过点B.当D′E⊥CD时,CE=1,则AB的长是$\frac{3\sqrt{3}+5}{2}$.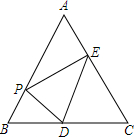 如图,在等边三角形ABC中,AB=6,点P是AB边上的任意一点(点P不与点A、点B重合),过点P作PD⊥AB,交直线BC于点D,作PE⊥AC,垂足为点F.
如图,在等边三角形ABC中,AB=6,点P是AB边上的任意一点(点P不与点A、点B重合),过点P作PD⊥AB,交直线BC于点D,作PE⊥AC,垂足为点F. 如图,方格中有一条美丽可爱的小鱼.
如图,方格中有一条美丽可爱的小鱼.