题目内容
3.已知抛物线y=ax2+bx+c(a≠0)与平行于x轴的直线交于A、B两点,若点A的坐标为(-2,8),线段AB=8,则$\frac{b}{a}$=-4或12.分析 根据题意求得B的坐标,即可求得对称轴x=-$\frac{b}{2a}$的值,即可求得$\frac{b}{a}$的值.
解答 解:∵AB∥x轴,A(-2,8),AB=8,
∴B(6,8)或(-10,8),
当B为(6,8)时,对称轴x=-$\frac{b}{2a}$=$\frac{-2+6}{2}$=2,
∴$\frac{b}{a}$=-4,
当B为(-10,8)时,对称轴x=-$\frac{b}{2a}$=$\frac{-10-2}{2}$=-6,
∴$\frac{b}{a}$=12;
故答案为-4或12.
点评 本题考查了二次函数图象上的坐标特征,根据坐标特征求得B的坐标是解题的关键.

练习册系列答案
相关题目
11.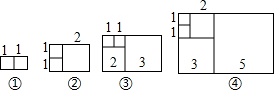 如图矩形都是由大小不等的正方形按照一定规律组成的,其中,第①个矩形的周长为6,第②个矩形的周长为10,第③个矩形的周长为16,…,则第⑧个矩形的周长为( )
如图矩形都是由大小不等的正方形按照一定规律组成的,其中,第①个矩形的周长为6,第②个矩形的周长为10,第③个矩形的周长为16,…,则第⑧个矩形的周长为( )
 如图矩形都是由大小不等的正方形按照一定规律组成的,其中,第①个矩形的周长为6,第②个矩形的周长为10,第③个矩形的周长为16,…,则第⑧个矩形的周长为( )
如图矩形都是由大小不等的正方形按照一定规律组成的,其中,第①个矩形的周长为6,第②个矩形的周长为10,第③个矩形的周长为16,…,则第⑧个矩形的周长为( )| A. | 168 | B. | 170 | C. | 178 | D. | 188 |
8. 如图这个立体图形的俯视图正确的是( )
如图这个立体图形的俯视图正确的是( )
 如图这个立体图形的俯视图正确的是( )
如图这个立体图形的俯视图正确的是( )| A. |  | B. |  | C. |  | D. |  |
12. 如图,直线a,b被直线c所截,a∥b,若∠1=75°,则∠2的度数为( )
如图,直线a,b被直线c所截,a∥b,若∠1=75°,则∠2的度数为( )
 如图,直线a,b被直线c所截,a∥b,若∠1=75°,则∠2的度数为( )
如图,直线a,b被直线c所截,a∥b,若∠1=75°,则∠2的度数为( )| A. | 15° | B. | 75° | C. | 105° | D. | 无法确定 |
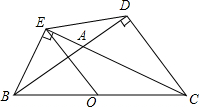 如图,△BCD和△BCE中,∠BDC=∠BEC=90°,O为BC的中点,BD,CE交于A,∠BAC=120°,求证:DE=OE.
如图,△BCD和△BCE中,∠BDC=∠BEC=90°,O为BC的中点,BD,CE交于A,∠BAC=120°,求证:DE=OE.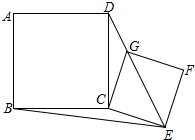 将边长为$\sqrt{5}$的正方形ABCD与边长为$\sqrt{2}$的正方形CEFG如图摆放,点G恰好落在线段DE上.连BE,则BE长为$\sqrt{13}$.
将边长为$\sqrt{5}$的正方形ABCD与边长为$\sqrt{2}$的正方形CEFG如图摆放,点G恰好落在线段DE上.连BE,则BE长为$\sqrt{13}$. 抛物线y=ax2+bx+c(a≠0)与x轴交于A(2,0),B(4,0)两点,与y轴交于点C(0,2).
抛物线y=ax2+bx+c(a≠0)与x轴交于A(2,0),B(4,0)两点,与y轴交于点C(0,2).