题目内容
3. 如图,正方形ABCD的边长为4,点E是正方形外一动点,∠AED=45°,P为AB的中点,当E运动时,线段PE的最大值为( )
如图,正方形ABCD的边长为4,点E是正方形外一动点,∠AED=45°,P为AB的中点,当E运动时,线段PE的最大值为( )| A. | 4$\sqrt{3}$ | B. | 3$\sqrt{2}$ | C. | 2+2$\sqrt{3}$ | D. | 2+2$\sqrt{2}$ |
分析 连接AC,BD交于点O,连接PO,EO,根据A,C,E,D四点共圆,可得OE=OD=$\frac{1}{2}$BD=2$\sqrt{2}$,再根据PE≤OP+OE=2+2$\sqrt{2}$,可得当点O在线段PE上时,PE=OP+OE=2+2$\sqrt{2}$,即线段PE的最大值为2+2$\sqrt{2}$.
解答 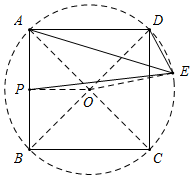 解:如图,连接AC,BD交于点O,连接PO,EO,
解:如图,连接AC,BD交于点O,连接PO,EO,
∵∠AED=45°,∠ACD=45°,
∴A,C,E,D四点共圆,
∵正方形ABCD的边长为4,
∴OE=OD=$\frac{1}{2}$BD=2$\sqrt{2}$,
∵P为AB的中点,O是BD的中点,
∴OP=$\frac{1}{2}$AD=2,
∵PE≤OP+OE=2+2$\sqrt{2}$,
∴当点O在线段PE上时,PE=OP+OE=2+2$\sqrt{2}$,
即线段PE的最大值为2+2$\sqrt{2}$,
故选:D.
点评 本题主要考查了正方形的性质、四点共圆、圆周角定理等知识的综合应用;熟练掌握正方形的性质,证明四点共圆是解决问题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
11.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{2}$×$\sqrt{8}$=4 | C. | $\sqrt{6}$÷$\sqrt{5}$=$\frac{\sqrt{6}}{5}$ | D. | $\sqrt{(-3)^{2}}$=-3 |
 如图,CD是△ABC角平分线,DE∥BC.若∠B=80°,∠A=60°,求∠CDE的度数.
如图,CD是△ABC角平分线,DE∥BC.若∠B=80°,∠A=60°,求∠CDE的度数. 已知如图为一几何体从不同方向看到的图形.
已知如图为一几何体从不同方向看到的图形.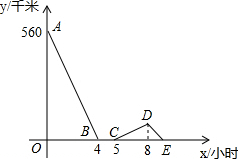 一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车,设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车,设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题: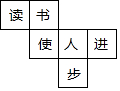 小强制作了一个正方体模型的展开图,如图所示,把“读书使人进步”六个字分别粘贴在六个面上,那么在正方体模型中与“书”相对的面上的字是( )
小强制作了一个正方体模型的展开图,如图所示,把“读书使人进步”六个字分别粘贴在六个面上,那么在正方体模型中与“书”相对的面上的字是( )