题目内容
14．
已知如图为一几何体从不同方向看到的图形．（1）写出这个几何体的名称；
（2）任意画出这个几何体的一种表面展开图；
（3）若长方形的高为8厘米，三角形的边长为3厘米，求这个几何体的侧面积．
分析 （1）只有棱柱的主视图和左视图才能出现长方形，根据俯视图是三角形，可得到此几何体为三棱柱；
（2）应该会出现三个长方形，两个三角形；
（3）侧面积为长方形，它的长和宽分别为3×3、8，计算出一个长方形的面积．
解答 解：（1）正三棱柱；
（2）展开图如下：
（3）这个几何体的侧面积为3×8×3=72（平方厘米）．
点评 本题主要考查由三视图判断几何体，用到的知识点为：棱柱的侧面都是长方形，上下底面是几边形就是几棱柱．
练习册系列答案
相关题目
1．若（2x+3）（x-4）=2x2+ax-b，则a，b的值分别是（ ）
| A． | a=-5，b=-12 | B． | a=-5，b=12 | C． | a=5，b=12 | D． | a=5，b=-12 |
2．下面的叙述正确的个数为（ ）
①若∠α=∠β，则∠α和∠β是一对对顶角；②若∠α与∠β互为补角，则∠α+∠β=180°；③一个角的补角比这个角的余角大90°；④同旁内角相等，两直线平行．
①若∠α=∠β，则∠α和∠β是一对对顶角；②若∠α与∠β互为补角，则∠α+∠β=180°；③一个角的补角比这个角的余角大90°；④同旁内角相等，两直线平行．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
3．
如图，正方形ABCD的边长为4，点E是正方形外一动点，∠AED=45°，P为AB的中点，当E运动时，线段PE的最大值为（ ）
如图，正方形ABCD的边长为4，点E是正方形外一动点，∠AED=45°，P为AB的中点，当E运动时，线段PE的最大值为（ ）| A． | 4$\sqrt{3}$ | B． | 3$\sqrt{2}$ | C． | 2+2$\sqrt{3}$ | D． | 2+2$\sqrt{2}$ |
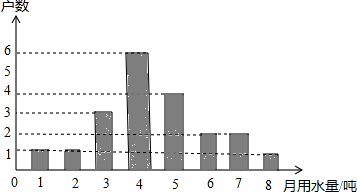张小花是社区宣传干部，为宣传节约用水，他随机调查了某小区部分家庭5月份的用水情况，并将收集的数据整理成如图的统计图．