题目内容
13. 如图,CD是△ABC角平分线,DE∥BC.若∠B=80°,∠A=60°,求∠CDE的度数.
如图,CD是△ABC角平分线,DE∥BC.若∠B=80°,∠A=60°,求∠CDE的度数.
分析 根据三角形内角和定理求出∠ACB,根据角平分线的定义求出∠BCD,根据平行线的性质解答即可.
解答 解:∵∠B=80°,∠A=60°,
∴∠ACB=180°-(∠B+∠A)=40°,
∵CD是△ABC角平分线,
∴∠BCD=$\frac{1}{2}$∠ACB=20°,
∵DE∥BC,
∴∠CDE=∠BCD=20°.
点评 本题考查的是三角形内角和定理、平行线的性质,掌握角平分线的定义、平行线的性质是解题的关键.

练习册系列答案
相关题目
20.若一个数的立方根和算术平方根都等于它本身,则这个数一定是( )
| A. | 0或1 | B. | 1或-1 | C. | 0或±1 | D. | 0 |
1.若(2x+3)(x-4)=2x2+ax-b,则a,b的值分别是( )
| A. | a=-5,b=-12 | B. | a=-5,b=12 | C. | a=5,b=12 | D. | a=5,b=-12 |
2.下面的叙述正确的个数为( )
①若∠α=∠β,则∠α和∠β是一对对顶角;②若∠α与∠β互为补角,则∠α+∠β=180°;③一个角的补角比这个角的余角大90°;④同旁内角相等,两直线平行.
①若∠α=∠β,则∠α和∠β是一对对顶角;②若∠α与∠β互为补角,则∠α+∠β=180°;③一个角的补角比这个角的余角大90°;④同旁内角相等,两直线平行.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3. 如图,正方形ABCD的边长为4,点E是正方形外一动点,∠AED=45°,P为AB的中点,当E运动时,线段PE的最大值为( )
如图,正方形ABCD的边长为4,点E是正方形外一动点,∠AED=45°,P为AB的中点,当E运动时,线段PE的最大值为( )
 如图,正方形ABCD的边长为4,点E是正方形外一动点,∠AED=45°,P为AB的中点,当E运动时,线段PE的最大值为( )
如图,正方形ABCD的边长为4,点E是正方形外一动点,∠AED=45°,P为AB的中点,当E运动时,线段PE的最大值为( )| A. | 4$\sqrt{3}$ | B. | 3$\sqrt{2}$ | C. | 2+2$\sqrt{3}$ | D. | 2+2$\sqrt{2}$ |
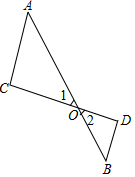 如图,AB与CD相交于点O,∠A=∠1,∠B=∠2.求证:AC∥DB.
如图,AB与CD相交于点O,∠A=∠1,∠B=∠2.求证:AC∥DB.