题目内容
13.在平面直角坐标系中,点A在y轴正半轴上.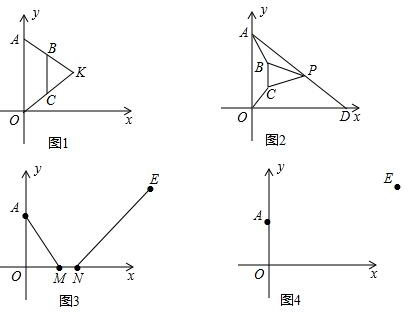
(1)如图1,以OA为底边向第一象限作等腰△OAK,直线BC∥y轴,交AK,OK分别于点B,C.求证:AB=OC;
(2)如图2,点D(2a,0),(a>0),点P(a,b)在线段AD上,连接PB,PC,求证:PB=PC;
(3)如图3(示意草图),已知A(0,2),E(6,3),M(m,0),N(m+1,0),若AM+MN+NE最小,请在备用图中画出线段MN(保留主要画图痕迹),并求出点M的坐标.
分析 (1)只要证明∠CBK=∠BCK,推出BK=CK,根据KA=KC,即可推出AB=OC;
(2)如图2中,连接PO.只要证明△PAB≌△POC即可解决问题;
(3)如图4中,将点A向右平移1个单位得到A′,作点A′关于x轴的对称点A″,连接A″E交x轴于N,点N向左平移1个单位得到点M,则此时AM+MN+NE的值最小.求出直线A″E的解析式,求出点N的坐标即可解决问题;
解答 解:(1)如图1中,
∵KA=KO,
∴∠KAO=∠KOA,
∵BC∥OA,
∴∠CBK=∠OAK,∠BCK=∠AOK,
∴∠CBK=∠BCK,
∴BK=CK,
∵KA=KO,
∴AB=OC.
(2)如图2中,连接PO.
∵点D(2a,0),(a>0),点P(a,b)在线段AD上,
∴PA=PD,∵∠AOD=90°,
∴PO=PA=PB,
∴∠PAO=∠POA,
∵∠BAC=∠COA(由(1)可知,
∴∠PAB=∠POC,
∵BA=OC(已证),
∴△PAB≌△POC,
∴PB=PC.
(3)如图4中,将点A向右平移1个单位得到A′,作点A′关于x轴的对称点A″,连接A″E交x轴于N,点N向左平移1个单位得到点M,则此时AM+MN+NE的值最小.
易知A″(1,-2),E(6,3),
设直线A″E的解析式为y=kx+b,则有$\left\{\begin{array}{l}{k+b=-2}\\{6k+b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$,
∴y=x-3,
∴N(3,0),
∵MN=1,
∴点M的坐标为(2,0).
点评 本题考查三角形综合题、全等三角形的判定和性质、等腰三角形的判定和性质、两点之间线段最短、一次函数的应用等知识,解题的关键是灵活运用所学知识解决问题,学会利用的长解决最短问题,学会添加辅助线构造全等三角形解决问题,属于中考压轴题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,正方形ABCD的边长为4,点E是正方形外一动点,∠AED=45°,P为AB的中点,当E运动时,线段PE的最大值为( )
如图,正方形ABCD的边长为4,点E是正方形外一动点,∠AED=45°,P为AB的中点,当E运动时,线段PE的最大值为( )| A. | 4$\sqrt{3}$ | B. | 3$\sqrt{2}$ | C. | 2+2$\sqrt{3}$ | D. | 2+2$\sqrt{2}$ |
| A. | 1的平方根是±1 | B. | -1的立方根是-1 | ||
| C. | $\sqrt{2}$是2的算术平方根 | D. | $\sqrt{(-3)^{2}}$的平方根是-3 |
| A. | 3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$ | B. | 2+$\sqrt{2}$=2$\sqrt{2}$ | C. | $\frac{\sqrt{12}-\sqrt{10}}{2}$=$\sqrt{6}-\sqrt{5}$ | D. | $\sqrt{2}+\sqrt{3}$=$\sqrt{5}$ |
 如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,不能推出四边形ABCD是矩形的是( )
如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,不能推出四边形ABCD是矩形的是( )| A. | BC=$\sqrt{3}$CD | B. | ∠A=90° | C. | AD=BC | D. | AB∥CD |
| A. | 当x=4时,式子有最大值-17 | B. | 当x=4时,式子有最小值-17 | ||
| C. | 当x=2时,式子有最大值-13 | D. | 当x=2时,式子有最小值-13 |
| A. | 4cm | B. | 5cm | C. | 小于2cm | D. | 不大于2cm |
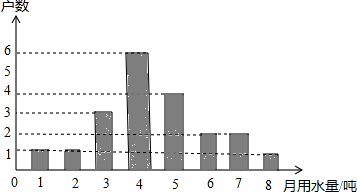 张小花是社区宣传干部,为宣传节约用水,他随机调查了某小区部分家庭5月份的用水情况,并将收集的数据整理成如图的统计图.
张小花是社区宣传干部,为宣传节约用水,他随机调查了某小区部分家庭5月份的用水情况,并将收集的数据整理成如图的统计图. 解不等式7+x≥2(2x-1),并把解集在如图的数轴上表示出来.
解不等式7+x≥2(2x-1),并把解集在如图的数轴上表示出来.