题目内容
18．已知直线l过A（2，0），且与直线y=2x+3平行，则直线l的解析式为y=2x-4．分析 两条平行线的则此两条直线的比例系数相同，故可设所求直线l的方程为y=2x+b，然后利用待定系数法求其解析式．
解答 解：∵直线l与y=2x+3平行，
∴设所求直线l的方程为y=2x+b；
又∵直线l过点（2，0），
∴0=2×2+b，
解得，b=-4，
∴所求的直线l的解析式为：y=2x-4．
故答案为：y=2x-4．
点评 本题考查了两直线平行的问题，熟记平行直线的解析式的k值相等是解题的关键．
练习册系列答案
同步练习强化拓展系列答案
相关题目
13．点A（1，m）为直线y=2x上一点，则OA的长度为（ ）
| A． | 1 | B． | $\sqrt{3}$ | C． | 2 | D． | $\sqrt{5}$ |
3．
如图，正方形ABCD的边长为4，点E是正方形外一动点，∠AED=45°，P为AB的中点，当E运动时，线段PE的最大值为（ ）
如图，正方形ABCD的边长为4，点E是正方形外一动点，∠AED=45°，P为AB的中点，当E运动时，线段PE的最大值为（ ）| A． | 4$\sqrt{3}$ | B． | 3$\sqrt{2}$ | C． | 2+2$\sqrt{3}$ | D． | 2+2$\sqrt{2}$ |
10．在实数$\sqrt{3}$，-2，0，$-\sqrt{2}$中，最大值是（ ）
| A． | $\sqrt{3}$ | B． | -2 | C． | 0 | D． | $-\sqrt{2}$ |
7．
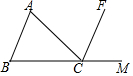如图，点C在射线BM上，CF是∠ACM的平分线，且CF∥AB，∠ACB=50°，则∠B的度数为（ ）
如图，点C在射线BM上，CF是∠ACM的平分线，且CF∥AB，∠ACB=50°，则∠B的度数为（ ）| A． | 65° | B． | 60° | C． | 55° | D． | 50° |
8．下列各式中计算正确的是（ ）
| A． | 3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$ | B． | 2+$\sqrt{2}$=2$\sqrt{2}$ | C． | $\frac{\sqrt{12}-\sqrt{10}}{2}$=$\sqrt{6}-\sqrt{5}$ | D． | $\sqrt{2}+\sqrt{3}$=$\sqrt{5}$ |