题目内容
14.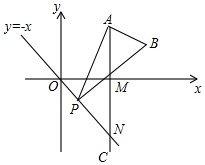 如图,已知点A($2\sqrt{3}$,3),AC⊥x轴于点M,交直线y=-x于点N,若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动,则当点P从点O运动到点N时,点B运动的路径长为2$\sqrt{2}$.
如图,已知点A($2\sqrt{3}$,3),AC⊥x轴于点M,交直线y=-x于点N,若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动,则当点P从点O运动到点N时,点B运动的路径长为2$\sqrt{2}$.
分析 首先,需要证明线段B0Bn就是点B运动的路径(或轨迹),如答图②所示.利用相似三角形可以证明;其次,如答图①所示,利用相似三角形△AB0Bn∽△AON,求出线段B0Bn的长度,即点B运动的路径长.
解答 解:由题意可知,OM=2$\sqrt{3}$,点N在直线y=-x上,AC⊥x轴于点M,
则△OMN为等腰直角三角形,ON=$\sqrt{2}$OM=$\sqrt{2}$×2$\sqrt{3}$=2$\sqrt{6}$.
如答图① 所示,
所示,
设动点P在O点(起点)时,点B的位置为B0,动点P在N点(终点)时,点B的位置为Bn,连接B0Bn.
∵AO⊥AB0,AN⊥ABn,
∴∠OAC=∠B0ABn,
又∵AB0=AO•tan30°,ABn=AN•tan30°,
∴AB0:AO=ABn:AN=tan30°(此处也可用30°角的Rt△三边长的关系来求得),
∴△AB0Bn∽△AON,且相似比为tan30°,
∴B0Bn=ON•tan30°=2$\sqrt{6}$×$\frac{\sqrt{3}}{3}$=2$\sqrt{2}$.
现在来证明线段B0Bn就是点B运动的路径(或轨迹).
如答图② 所示,
所示,
当点P运动至ON上的任一点时,设其对应的点B为Bi,连接AP,ABi,B0Bi.
∵AO⊥AB0,AP⊥ABi,
∴∠OAP=∠B0ABi,
又∵AB0=AO•tan30°,ABi=AP•tan30°,
∴AB0:AO=ABi:AP,
∴△AB0Bi∽△AOP,
∴∠AB0Bi=∠AOP.
又∵△AB0Bn∽△AON,
∴∠AB0Bn=∠AOP,
∴∠AB0Bi=∠AB0Bn,
∴点Bi在线段B0Bn上,即线段B0Bn就是点B运动的路径(或轨迹).
综上所述,点B运动的路径(或轨迹)是线段B0Bn,其长度为2$\sqrt{2}$,
故答案为:2$\sqrt{2}$.
点评 本题考查坐标平面内由相似关系确定的点的运动轨迹,难度很大.本题的要点有两个:首先,确定点B的运动路径是本题的核心,这要求考生有很好的空间想象能力和分析问题的能力;其次,由相似关系求出点B运动路径的长度,可以大幅简化计算,避免陷入坐标关系的复杂运算之中.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案| A. | 2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | -2 |
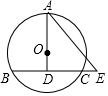 如图,⊙O的半径为5,弦BC=8,点A在⊙O上,AO⊥BC,垂足为D、E为BC延长线上一点,AE=10,则CE的长为2.
如图,⊙O的半径为5,弦BC=8,点A在⊙O上,AO⊥BC,垂足为D、E为BC延长线上一点,AE=10,则CE的长为2.
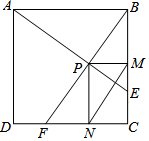 如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,
如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,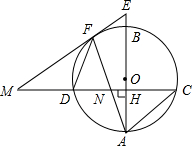 如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.
如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.