题目内容
2．一个不透明的口袋中装有四个完全相同的小球，把它们分别标号为1，2，3，4．从袋中随机摸出一只小球，再从剩下的小球中随机摸出一只小球，请用列表法或画树形图的方法，求两次摸出的小球上所标数字之和大于4的概率．分析 通过列表展示12种等可能的结果数，再找出所标数字之和大于4的所占结果数，然后根据概率公式计算．
解答 解：列表如下：
| 1 | 2 | 3 | 4 | |
| 1 | （1，2） | （1，3） | （1，4） | |
| 2 | （2，1） | （2，3） | （2，4） | |
| 3 | （3，1） | （3，2） | （3，4） | |
| 4 | （4，1） | （4，2） | （4，3） |
所以 P（数字之和大于4）=$\frac{8}{12}$=$\frac{2}{3}$．
点评 本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A或B的结果数目m，然后利用概率公式求事件A或B的概率．
练习册系列答案
口算小状元口算速算天天练系列答案
天天练口算系列答案
相关题目
13．某市园林部门为了扩大城市的绿化面积，进行了大量的树木移栽，下表记录的是在相同的条件下移栽某种幼树的棵树与成活棵树：
依此估计这种幼树成活的概率是0.9．（结果用小数表示，精确到0.1）
| 移栽棵树 | 100 | 1000 | 10000 | 20000 |
| 成活棵树 | 89 | 910 | 9008 | 18004 |
17．“…日啖荔枝三百颗，不辞长作岭南人”．是荔枝在运输、储存中会有损坏，下表是销售人员随机抽取若干荔枝，进行荔枝损坏率的统计的一组数据．
估计荔枝损坏的概率是0.1答案不唯一．
| 荔枝总质量n/Kg | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
| 损坏荔枝质量m/Kg | 5.50 | 10.50 | 15.15 | 19.42 | 24.25 | 30.93 | 35.32 | 39.24 | 44.57 | 51.51 |
| 荔枝损坏的频率$\frac{m}{n}$ | 0.110 | 0.105 | 0.101 | 0.097 | 0.097 | 0.103 | 0.101 | 0.098 | 0.099 | 0.103 |
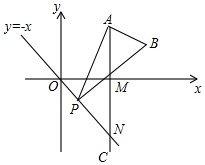如图，已知点A（$2\sqrt{3}$，3），AC⊥x轴于点M，交直线y=-x于点N，若点P是线段ON上的一个动点，∠APB=30°，BA⊥PA，则点P在线段ON上运动时，A点不变，B点随之运动，则当点P从点O运动到点N时，点B运动的路径长为2$\sqrt{2}$．