题目内容
4.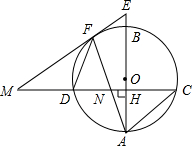 如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.
如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.(1)求证:CA=CN;
(2)连接DF,若cos∠DFA=$\frac{4}{5}$,AN=2$\sqrt{10}$,求圆O的直径的长度.
分析 (1)连接OF,根据切线的性质结合四边形内角和为360°,即可得出∠M+∠FOH=180°,由三角形外角结合平行线的性质即可得出∠M=∠C=2∠OAF,再通过互余利用角的计算即可得出∠CAN=90°-∠OAF=∠ANC,由此即可证出CA=CN;
(2)连接OC,由圆周角定理结合cos∠DFA=$\frac{4}{5}$、AN=2$\sqrt{10}$,即可求出CH、AH的长度,设圆的半径为r,则OH=r-6,根据勾股定理即可得出关于r的一元一次方程,解之即可得出r,再乘以2即可求出圆O直径的长度.
解答 (1)证明:连接OF,则∠OAF=∠OFA,如图所示.
∵ME与⊙O相切,
∴OF⊥ME.
∵CD⊥AB,
∴∠M+∠FOH=180°.
∵∠BOF=∠OAF+∠OFA=2∠OAF,∠FOH+∠BOF=180°,
∴∠M=2∠OAF.
∵ME∥AC,
∴∠M=∠C=2∠OAF.
∵CD⊥AB,
∴∠ANC+∠OAF=∠BAC+∠C=90°,
∴∠ANC=90°-∠OAF,∠BAC=90°-∠C=90°-2∠OAF,
∴∠CAN=∠OAF+∠BAC=90°-∠OAF=∠ANC,
∴CA=CN.
(2)连接OC,如图2所示.
∵cos∠DFA=$\frac{4}{5}$,∠DFA=∠ACH,
∴$\frac{CH}{AC}$=$\frac{4}{5}$.
设CH=4a,则AC=5a,AH=3a,
∵CA=CN,
∴NH=a,
∴AN=$\sqrt{A{H}^{2}+N{H}^{2}}$=$\sqrt{(3a)^{2}+{a}^{2}}$=$\sqrt{10}$a=2$\sqrt{10}$,
∴a=2,AH=3a=6,CH=4a=8.
设圆的半径为r,则OH=r-6,
在Rt△OCH中,OC=r,CH=8,OH=r-6,
∴OC2=CH2+OH2,r2=82+(r-6)2,
解得:r=$\frac{25}{3}$,
∴圆O的直径的长度为2r=$\frac{50}{3}$.
点评 本题考查了切线的性质、勾股定理、解直角三角形、圆周角定理以及解一元一次方程,解题的关键是:(1)通过角的计算找出∠CAN=90°-∠OAF=∠ANC;(2)利用解直角三角形求出CH、AH的长度.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案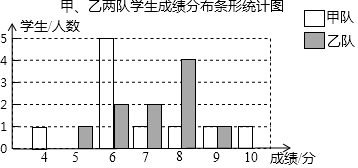
根据以上信息,请解答下面的问题:
(1)在下面甲、乙两队的成绩统计表中,a=6.8,b=7.5c=6.
| 平均分 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 | |
| 甲队 | a | 6 | c | 2.76 | 90% | 20% |
| 乙队 | 7.2 | b | 8 | 1.36 | 80% | 10% |
(3)甲队同学认为:甲队的合格率、优秀率均高于乙队,所以甲队的成绩好于乙队.但乙队同学不同意甲队同学的说法,认为乙队的成绩要好于甲队.请你写出两条支持乙队同学观点的理由.
(4)学校要从从甲、乙两队获得优秀的学生中,选取两名同学参加市级比赛,则恰好同时选中的两人均为甲队学生的概率为$\frac{1}{3}$.
| A. | 2 | B. | $\sqrt{5}$ | C. | 3 | D. | 4 |
| A. | 众数是3 | B. | 平均数是4 | C. | 方差是1.6 | D. | 中位数是6 |
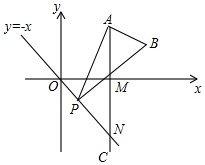 如图,已知点A($2\sqrt{3}$,3),AC⊥x轴于点M,交直线y=-x于点N,若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动,则当点P从点O运动到点N时,点B运动的路径长为2$\sqrt{2}$.
如图,已知点A($2\sqrt{3}$,3),AC⊥x轴于点M,交直线y=-x于点N,若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动,则当点P从点O运动到点N时,点B运动的路径长为2$\sqrt{2}$.
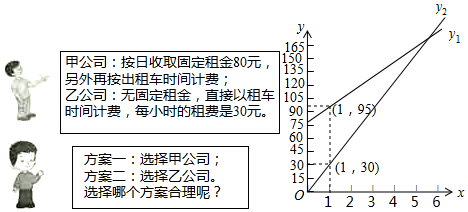 “五•一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
“五•一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.