题目内容
3.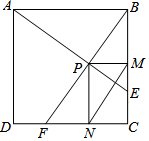 如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,
如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,①AE和BF的位置关系为AE⊥BF.;
②线段MN的最小值为$\frac{\sqrt{5}-1}{2}$.
分析 ①由△ABE≌△BCF(SAS),推出∠BAE=∠CBF,AE=BF,由∠BAE+∠BEA=90°,推出∠CBF+∠BEA=90°,推出∠APB=90°;
②由点P在运动中保持∠APB=90°,推出点P的路径是一段以AB为直径的弧,设AB的中点为G,连接CG交弧于点P,此时CP的长度最小;
解答 解:①如图,∵动点F,E的速度相同,
∴DF=CE,
又∵CD=BC,
∴CF=BE,
在△ABE和△BCF中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠BCF=90°}\\{BE=CF}\end{array}\right.$,
∴△ABE≌△BCF(SAS),
∴∠BAE=∠CBF,AE=BF,
∵∠BAE+∠BEA=90°,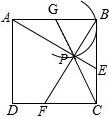
∴∠CBF+∠BEA=90°,
∴∠APB=90°,
∴AE⊥BF,
②∵点P在运动中保持∠APB=90°,
∴点P的路径是一段以AB为直径的弧,
设AB的中点为G,连接CG交弧于点P,此时CP的长度最小,
在Rt△BCG中,CG=$\sqrt{B{C}^{2}+B{G}^{2}}$=$\sqrt{1+(\frac{1}{2})^{2}}$=$\frac{\sqrt{5}}{2}$,
∵PG=$\frac{1}{2}$AB=$\frac{1}{2}$,
∴CP=CG-PG=$\frac{\sqrt{5}}{2}$-$\frac{1}{2}$=$\frac{\sqrt{5}-1}{2}$,
即线段CP的最小值为 $\frac{\sqrt{5}-1}{2}$,
故答案为AE⊥BF,$\frac{\sqrt{5}-1}{2}$.
点评 本题为四边形的综合应用,涉及全等三角形、勾股定理、正方形的性质、圆的有关知识等知识点.在判定三角形全等时,关键是选择恰当的判定条件,学会利用辅助圆解决问题,掌握求圆外一点到圆的点的距离的最值问题的方法,属于中考填空题中的压轴题.

| 移栽棵树 | 100 | 1000 | 10000 | 20000 |
| 成活棵树 | 89 | 910 | 9008 | 18004 |
 关于右面两个几何体的视图,正确的说法是( )
关于右面两个几何体的视图,正确的说法是( )| A. | 它们的主视图相同 | B. | 它们的俯视图相同 | ||
| C. | 它们的左视图不同 | D. | 它们的三种视图均不同 |
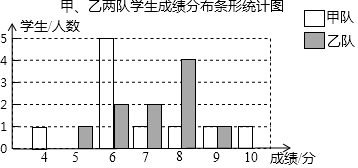
根据以上信息,请解答下面的问题:
(1)在下面甲、乙两队的成绩统计表中,a=6.8,b=7.5c=6.
| 平均分 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 | |
| 甲队 | a | 6 | c | 2.76 | 90% | 20% |
| 乙队 | 7.2 | b | 8 | 1.36 | 80% | 10% |
(3)甲队同学认为:甲队的合格率、优秀率均高于乙队,所以甲队的成绩好于乙队.但乙队同学不同意甲队同学的说法,认为乙队的成绩要好于甲队.请你写出两条支持乙队同学观点的理由.
(4)学校要从从甲、乙两队获得优秀的学生中,选取两名同学参加市级比赛,则恰好同时选中的两人均为甲队学生的概率为$\frac{1}{3}$.
| A. | 众数是3 | B. | 平均数是4 | C. | 方差是1.6 | D. | 中位数是6 |
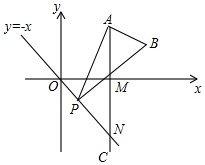 如图,已知点A($2\sqrt{3}$,3),AC⊥x轴于点M,交直线y=-x于点N,若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动,则当点P从点O运动到点N时,点B运动的路径长为2$\sqrt{2}$.
如图,已知点A($2\sqrt{3}$,3),AC⊥x轴于点M,交直线y=-x于点N,若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动,则当点P从点O运动到点N时,点B运动的路径长为2$\sqrt{2}$.