题目内容
4.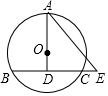 如图,⊙O的半径为5,弦BC=8,点A在⊙O上,AO⊥BC,垂足为D、E为BC延长线上一点,AE=10,则CE的长为2.
如图,⊙O的半径为5,弦BC=8,点A在⊙O上,AO⊥BC,垂足为D、E为BC延长线上一点,AE=10,则CE的长为2.
分析 连接OC,根据垂径定理得到BD=DC=$\frac{1}{2}$BC=4,根据勾股定理求出OD,根据勾股定理求出DE,计算即可.
解答 解:连接OC,
∵AO⊥BC,
∴BD=DC=$\frac{1}{2}$BC=4,
∴OD=$\sqrt{O{C}^{2}-D{C}^{2}}$=3,
则AD=AO+OD=8,
∴DE=$\sqrt{A{E}^{2}-A{D}^{2}}$=6,
∴CE=DE-DC=2,
故答案为:2.
点评 本题考查的是垂径定理、勾股定理的应用,掌握垂直弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.

练习册系列答案
相关题目
15. 下列左视图正确的是( )
下列左视图正确的是( )
 下列左视图正确的是( )
下列左视图正确的是( )| A. |  | B. |  | C. |  | D. |  |
13.某市园林部门为了扩大城市的绿化面积,进行了大量的树木移栽,下表记录的是在相同的条件下移栽某种幼树的棵树与成活棵树:
依此估计这种幼树成活的概率是0.9.(结果用小数表示,精确到0.1)
| 移栽棵树 | 100 | 1000 | 10000 | 20000 |
| 成活棵树 | 89 | 910 | 9008 | 18004 |
 如图,在菱形ABCD中,∠BAD=100°,点E为AC上一点,若∠CBE=20°,则∠AED=70°.
如图,在菱形ABCD中,∠BAD=100°,点E为AC上一点,若∠CBE=20°,则∠AED=70°.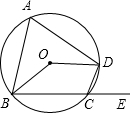 如图,四边形ABCD内接于⊙O,若∠BOD=130°,则它的一个外角∠DCE=65°.
如图,四边形ABCD内接于⊙O,若∠BOD=130°,则它的一个外角∠DCE=65°.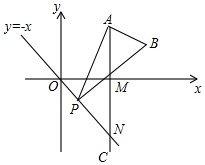 如图,已知点A($2\sqrt{3}$,3),AC⊥x轴于点M,交直线y=-x于点N,若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动,则当点P从点O运动到点N时,点B运动的路径长为2$\sqrt{2}$.
如图,已知点A($2\sqrt{3}$,3),AC⊥x轴于点M,交直线y=-x于点N,若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动,则当点P从点O运动到点N时,点B运动的路径长为2$\sqrt{2}$.