题目内容
19.甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动.(1)1月1日甲与乙同时开始攀登一座1800米高的山,甲比乙早30分钟到达顶峰.已知甲的平均攀登速度是乙的1.2倍,求甲的平均攀登速度是每分钟多少米?
(2)1月10日甲与丙去攀登另一座a米高的山,甲保持第(1)问中的速度不变,比丙晚出发1小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含a的代数式表示)
分析 (1)设乙的攀登速度为x米/分,则甲的速度为1.2x米/分,根据“甲比乙早30分钟到达顶峰”列出方程并解答.
(2)设丙的攀登速度为y米/分,根据“比丙晚出发1小时,结果两人同时到达顶峰”列出方程并解答.
解答 解:(1)设乙的攀登速度为x米/分,则甲的速度为1.2x米/分,
$\frac{1800}{1.2x}$+30=$\frac{1800}{x}$,
解得x=10,
检验:x=10是原分式方程的解,
所以1.2x=12,
答:甲的平均攀登速度是每分钟12米;
(2)设丙的攀登速度为y米/分,
依题意得:$\frac{a}{12}$+60=$\frac{a}{y}$,
解得$y=\frac{12a}{a+12}$,
检验:$y=\frac{12a}{a+12}$是原分式方程的解.
所以$\frac{12}{y}$=$\frac{a+720}{a}$.
所以甲的平均攀登速度是丙的$\frac{a+720}{a}$倍.
点评 本题考查了分式方程的应用.利用分式方程解应用题时,一般题目中会有两个相等关系,这时要根据题目所要解决的问题,选择其中的一个相等关系作为列方程的依据,而另一个则用来设未知数.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
10.若3a7xby+7与2a14b2x是同类项,则yx的值是( )
| A. | -9 | B. | -6 | C. | 6 | D. | 9 |
14.已知抛物线y=x2+bx+c的顶点在第三象限,则关于x的一元二次方程x2+bx+c=0根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
4.如图,有四个大小相同的小长方形和两个大小相同的大长方形按如图位置摆放,按照图中所示尺寸,则小长方形的长与宽的差是( )
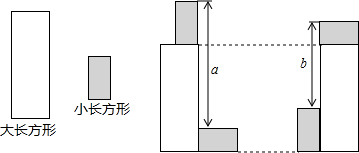

| A. | 3b-2a | B. | $\frac{a-b}{2}$ | C. | $\frac{a-b}{3}$ | D. | $\frac{a}{3}-\frac{b}{4}$ |
11.如果m是任意实数,那么点M(m-5,m+2)一定不在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.下列标志是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图是由5个大小相同的小正方体摆成的立体图形,则从正面看得到的平面图形是( )
如图是由5个大小相同的小正方体摆成的立体图形,则从正面看得到的平面图形是( )


