题目内容
14.已知抛物线y=x2+bx+c的顶点在第三象限,则关于x的一元二次方程x2+bx+c=0根的情况是( )| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
分析 根据抛物线y=x2+bx+c的顶点在第三象限,可以判断出b2-4ac的正负,从而可以得到一元二次方程x2+bx+c=0中△的正负,从而可以判断一元二次方程x2+bx+c=0的根的情况.
解答 解:∵抛物线y=x2+bx+c的顶点在第三象限,
∴-$\frac{b}{2×1}<0$,$\frac{4×1×c-{b}^{2}}{4×1}<0$,
∴b>0,4c-b2<0,
∴在一元二次方程x2+bx+c=0中,△=b2-4×1×c=b2-4c>0,
∴关于x的一元二次方程x2+bx+c=0有两个不相等的实数根,
故选A.
点评 本题考查抛物线与x轴的交点,解题的关键是明确二次函数与一元二次方程之间的关系,判断根的情况就要求△得值.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
9.在一个不透明的布袋中,红色、黑色、白色的乒乓球共有20个,除颜色外,形状、大小、质地等完全相同.小明通过多次摸球实验后发现其中投到红色、黑色球的频率稳定在5%和15%,则口袋中白色球的个数很可能是( )
| A. | 3个 | B. | 4个 | C. | 10个 | D. | 16个 |
6.下列各实数是无理数的是( )
| A. | $\sqrt{\frac{1}{4}}$ | B. | $\frac{29}{4}$ | C. | 3.$\stackrel{••}{05}$ | D. | -π |
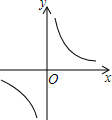 反比例函数y=$\frac{m}{x}$的图象如图所示,有下列结论:
反比例函数y=$\frac{m}{x}$的图象如图所示,有下列结论: 如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DC=3,则点D到AB的距离是( )
如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DC=3,则点D到AB的距离是( )