题目内容
16. 如图(1)所示,E为矩形ABCD的边AD上一点动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:
如图(1)所示,E为矩形ABCD的边AD上一点动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:①0<t≤5时,y=$\frac{4}{5}{t^2}$;
②当t=6秒时,△ABE≌△PQB;
③cos∠CBE=$\frac{4}{5}$;
④当t=$\frac{29}{2}$秒时,△ABE∽△QBP;
⑤线段NF所在直线的函数关系式为:y=-4x+96.
其中正确的是①②④.(填序号)
分析 根据图(2)可以判断三角形的面积变化分为四段,①当点P在BE上运动,点Q到达点C时;②当点P到达点E时,点Q静止于点C,从而得到BC、BE的长度;③点P到达点D时,点Q静止于点C;④当点P在线段CD上,点Q仍然静止于点C时.
解答 解:当0<t≤5时,点P在线段BE上运动.如图(1)所示:过点P作PF⊥BQ,垂足为F.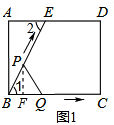
S△BPQ=$\frac{1}{2}$PF•BQ=$\frac{1}{2}$BP•sin∠CBE•BQ=$\frac{1}{2}$t•sin∠CBE•2t=sin∠CBEt2.
将(5,20)代入得25sin∠CBE=20,解得:sin∠CBE=$\frac{4}{5}$,
0<t≤5时,y=$\frac{4}{5}{t^2}$,故①正确.
∵sin∠CBE=$\frac{4}{5}$,
∴COS∠CBE=$\frac{3}{5}$,故③错误.
由图(2)可知:当t=5时,点Q与点C重合,当t=10时,点P与点E重合,则BC=10,BE=10.则BC=BE.
∵∠AEB=∠CBE,
∴AB=BEsin∠AEB=10×$\frac{4}{5}$=8.
在△ABE中,AE=$\sqrt{B{E}^{2}-A{B}^{2}}$=6.
当t=6时,如图2所示: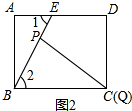
在△ABE与△PQB中,$\left\{\begin{array}{l}{AE=BP=6}\\{∠1=∠2}\\{BE=BC}\end{array}\right.$,
∴△ABE≌△PQB(SAS).
故②正确.
当t=$\frac{29}{2}$秒时,如图3所示: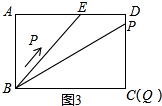
∵当t=$\frac{29}{2}$秒时,PD=$\frac{29}{2}$-14=$\frac{1}{2}$,
∴PQ=8-$\frac{1}{2}$=7.5.
∴$\frac{PQ}{BQ}=\frac{7.5}{10}=\frac{3}{4}$.
又∵$\frac{AE}{AB}=\frac{6}{8}=\frac{3}{4}$,
∴$\frac{PQ}{BQ}=\frac{AE}{AB}$.
又∵∠BQP=∠A,
∴△AEB∽△QBP.
故④正确.
由DC=8,可知点F(22,0)
设NF的解析式为y=kx+b.
将N、F的坐标代入得:$\left\{\begin{array}{l}{14k+b=40}\\{22k+b=0}\end{array}\right.$,
解得:k=-5,b=110.
∴NF所在直线解析式为y=-5x+110.
故⑤错误.
故答案为:①②④.
点评 本题考查了动点问题的函数图象,根据图(2)判断出点P到达点E用了10s,点Q到达点C用了5s是解题的关键,也是本题的突破口

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案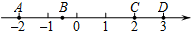 如图,数轴上有A,B,C,D四个点,其中绝对值小于2的数对应的点是( )
如图,数轴上有A,B,C,D四个点,其中绝对值小于2的数对应的点是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
 如图,△ABC中,AB=AC.
如图,△ABC中,AB=AC.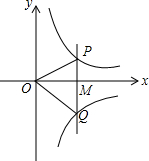 如图,若点M是x轴正半轴上的任意一点,过点M作PQ⊥x轴,分别交函数y=$\frac{4}{x}$(x>0)和y=-$\frac{6}{x}$(x>0)的图象于点P和Q,连接OP、OQ,则△POQ的面积为5.
如图,若点M是x轴正半轴上的任意一点,过点M作PQ⊥x轴,分别交函数y=$\frac{4}{x}$(x>0)和y=-$\frac{6}{x}$(x>0)的图象于点P和Q,连接OP、OQ,则△POQ的面积为5. 如图,∠A=∠E,AC⊥BE,AB=EF,BE=10,CF=4,则AC=6.
如图,∠A=∠E,AC⊥BE,AB=EF,BE=10,CF=4,则AC=6.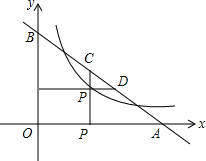 如图,点P是函数y=$\frac{2}{x}$(x>0)图象上的一点,直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点,过点P作x轴、y轴的垂线与该直线分别交于C、D两点,则AD•BC的值为$\frac{25}{6}$.
如图,点P是函数y=$\frac{2}{x}$(x>0)图象上的一点,直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点,过点P作x轴、y轴的垂线与该直线分别交于C、D两点,则AD•BC的值为$\frac{25}{6}$.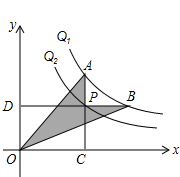 如图,反比例函数y=$\frac{5}{x}$和y=$\frac{3}{x}$,在第一象限内图象依次是Q1和Q2.设点P在Q2,直线PC⊥x轴于点C,交Q1于点A,直线PD⊥y轴于点D,交Q1于点B,连结OA,OB,则图中阴影部分的面积为2.
如图,反比例函数y=$\frac{5}{x}$和y=$\frac{3}{x}$,在第一象限内图象依次是Q1和Q2.设点P在Q2,直线PC⊥x轴于点C,交Q1于点A,直线PD⊥y轴于点D,交Q1于点B,连结OA,OB,则图中阴影部分的面积为2.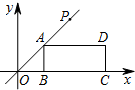 如图,在平面直角坐标系中,矩形ABCD的边BC在x轴的正半轴上,点B在点C的左侧,直线y=kx经过点A(3,3)和点P,且OP=6$\sqrt{2}$.将直线y=kx沿y轴向下平移得到直线y=kx+b,若点P落在矩形ABCD的内部,则b的取值范围是( )
如图,在平面直角坐标系中,矩形ABCD的边BC在x轴的正半轴上,点B在点C的左侧,直线y=kx经过点A(3,3)和点P,且OP=6$\sqrt{2}$.将直线y=kx沿y轴向下平移得到直线y=kx+b,若点P落在矩形ABCD的内部,则b的取值范围是( )