题目内容
11.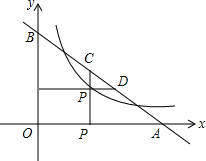 如图,点P是函数y=$\frac{2}{x}$(x>0)图象上的一点,直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点,过点P作x轴、y轴的垂线与该直线分别交于C、D两点,则AD•BC的值为$\frac{25}{6}$.
如图,点P是函数y=$\frac{2}{x}$(x>0)图象上的一点,直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点,过点P作x轴、y轴的垂线与该直线分别交于C、D两点,则AD•BC的值为$\frac{25}{6}$.
分析 设点P(m,$\frac{2}{m}$),则点C(m,-$\frac{3}{4}m$+3),点D(4-$\frac{8}{3m}$,$\frac{2}{m}$),求出线段AD、BC即可解决问题.
解答  解:∵直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点,
解:∵直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点,
∴点A(4,0),点B(0,3),
设点P(m,$\frac{2}{m}$),则点C(m,-$\frac{3}{4}m$+3),点D(4-$\frac{8}{3m}$,$\frac{2}{m}$),
∴AD=$\sqrt{(\frac{8}{3m})^{2}+(\frac{2}{m})^{2}}$=$\frac{10}{3m}$,BC=$\sqrt{{m}^{2}+(-\frac{3}{4}m)^{2}}$=$\frac{5}{4}m$,
∴AD•BC=$\frac{10}{3m}$•$\frac{5}{4}m$=$\frac{25}{6}$.
故答案为$\frac{25}{6}$.
点评 本题考查反比例函数图象上的点、一次函数、两点之间的距离公式等知识,解题的关键是设未知数,用未知数表示线段AD、BC,属于中考常考题型.

练习册系列答案
相关题目
1.若a为有理数,则a的倒数$\frac{1}{a}$( )
| A. | 一定是实数 | B. | 是无理数 | ||
| C. | 不存在 | D. | 当a≠0时,$\frac{1}{a}$一定是有理数 |
6.-(-1)的相反数的倒数是( )
| A. | 0 | B. | -1 | C. | 1 | D. | 不存在 |
3.下列计算正确的是( )
| A. | a+a2=a3 | B. | a6b÷a2=a3b | C. | (a-b)2=a2-b2 | D. | (-ab3)2=a2b6 |
20. 如图,等腰直角三角板的顶点A,C分别在直线a,b上.若a∥b,∠1=35°,则∠2的度数为( )
如图,等腰直角三角板的顶点A,C分别在直线a,b上.若a∥b,∠1=35°,则∠2的度数为( )
 如图,等腰直角三角板的顶点A,C分别在直线a,b上.若a∥b,∠1=35°,则∠2的度数为( )
如图,等腰直角三角板的顶点A,C分别在直线a,b上.若a∥b,∠1=35°,则∠2的度数为( )| A. | 35° | B. | 15° | C. | 10° | D. | 5° |
1.a的倒数是-1.5,则a是( )
| A. | -$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
 如图(1)所示,E为矩形ABCD的边AD上一点动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:
如图(1)所示,E为矩形ABCD的边AD上一点动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论: