题目内容
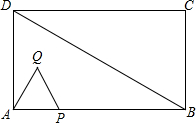 如图,在△ABD中,∠DAB=90°,∠ABD=30°,AD=2
如图,在△ABD中,∠DAB=90°,∠ABD=30°,AD=2| 3 |
(1)填空:
①AP=
②当Q点在线段DC上时,t=
(2)当线段PQ经过点C时,求出此时t的值.
考点:勾股定理,解直角三角形
专题:动点型
分析:(1)①根据路程=时间×速度填空即可;②求出DQ,即可求出AP,即可得出答案;
(2)求出BP,求出AP即可求出的值.
(2)求出BP,求出AP即可求出的值.
解答:解:(1)①∵P以每秒1个单位长度的速度在射线AB上运动,运动的时间为t秒,
∴AP=1•t=t,
故答案为:t;
②如图1,当Q点在线段DC上时,
∵AD=2
,∠ADQ=90°,∠DAQ=90°-60°=30°,
∴设DQ=x,则AQ=2x,
∴(2
)2+x2=(2x)2,
∴x=2,
∴AP=4,
∴t=4,
∴当t=4秒时,Q在线段DC上.
故答案为:4;
(2)如图2,当线段PQ经过点C时,
∵当C在PQ上时,点P在AB延长线上,由题意得:BP=
=
=2,
∴AP=AB+BP=6+2=8,
∴t=8,
∴当t=8秒时,点C在线段PQ上.
∴AP=1•t=t,

故答案为:t;
②如图1,当Q点在线段DC上时,
∵AD=2
| 3 |
∴设DQ=x,则AQ=2x,
∴(2
| 3 |
∴x=2,
∴AP=4,
∴t=4,
∴当t=4秒时,Q在线段DC上.
故答案为:4;
(2)如图2,当线段PQ经过点C时,
∵当C在PQ上时,点P在AB延长线上,由题意得:BP=
| BC |
| tan60° |
2
| ||
|
∴AP=AB+BP=6+2=8,
∴t=8,
∴当t=8秒时,点C在线段PQ上.
点评:本题考查了勾股定理,矩形的性质,等边三角形的性质和判定的应用,题目比较好,难度偏大,用了分类讨论思想.

练习册系列答案
相关题目
 张师傅划下一片阴影部分,弦AB长为240mm,CD最大为35mm.请求出原镜片的直径.
张师傅划下一片阴影部分,弦AB长为240mm,CD最大为35mm.请求出原镜片的直径.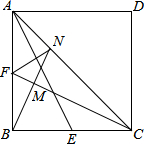 正方形ABCD中,点E、F分别是BC、AB边的中点,连接AE、CF,过点B作BM⊥FC交对角线AC于点N,连接FN,探究FN与AE的位置关系,并证明.
正方形ABCD中,点E、F分别是BC、AB边的中点,连接AE、CF,过点B作BM⊥FC交对角线AC于点N,连接FN,探究FN与AE的位置关系,并证明.