题目内容
两个多边形的边数之比为1：2，内角和之比为2：5，求这两个多边形的边数．
考点：多边形内角与外角
专题：
分析：本题考查根据多边形的内角和计算公式求多边形的边数．本题根据等量关系“内角和之比为2：5”列方程求解，解答时要会根据公式进行正确运算、变形和数据处理．
解答：解：设多边形较少的边数为n，则
[（n-2）•180°]：[（2n-2）•180°]=2：5，
解得n=6．
2n=12．
故这两个多边形的边数分别为6，12．
[（n-2）•180°]：[（2n-2）•180°]=2：5，
解得n=6．
2n=12．
故这两个多边形的边数分别为6，12．
点评：本题考查多边形的内角和、方程的思想．关键是记住内角和的公式．
练习册系列答案
相关题目
如图，在△ABC中，AB=8，AC=6，D在AB上，且AD=3，在AC上找一点P，使△APD∽△ABC，则AP=若x=2y-3，则2x-
（16y-20）的值是（ ）
| 1 |
| 4 |
| A、1 | B、-1 | C、11 | D、-11 |
有两个边长分别为a、b和c、d的长方形，其重叠部分为一边长为2的小正方形，则其它不重叠部分的面积为（ ）
| A、ab+cd-2 |
| B、ab+cd-4 |
| C、ab+cd-8 |
| D、ab+cd-16 |
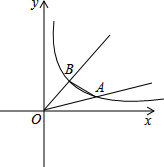如图，已知∠AOB在平面直角坐标系的第一象限中，且∠AOB=30°，其两边分别交反比例函数y=
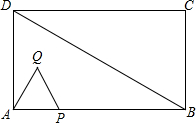如图，在△ABD中，∠DAB=90°，∠ABD=30°，AD=2
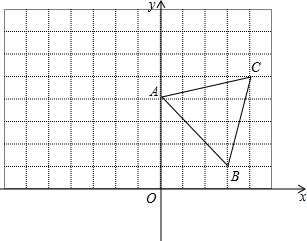已知在平面直角坐标系中，点A的坐标为（0，4），点B的坐标为（3，1），点C的坐标为（4，5），将△ABC绕原点O逆时针旋转90°，得到△A1B1C1，（其中点A转到点A1处，点B转到点B处）．