题目内容
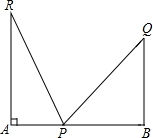 如图,设在一个宽度为AB的小巷内,一个梯子的长度为b,梯子的底部位于P点,当梯子靠在左面墙上时,顶端距底面的高为c,且梯子与底面的夹角为75°;靠在另一面墙上时,顶端距底面的高度为d,且梯子与底面的夹角为45°,求小巷的宽度AB.
如图,设在一个宽度为AB的小巷内,一个梯子的长度为b,梯子的底部位于P点,当梯子靠在左面墙上时,顶端距底面的高为c,且梯子与底面的夹角为75°;靠在另一面墙上时,顶端距底面的高度为d,且梯子与底面的夹角为45°,求小巷的宽度AB.考点:全等三角形的应用,等边三角形的判定与性质
专题:
分析:连接QR,过Q作QN⊥AR,则可证△PQR为等边三角形,得PQ=PR,进而求证△NQR≌△ARP,可得QN=RA,即墙面之间距离AB=c.
解答: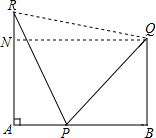 解:连接QR,过Q作QN⊥AR,
解:连接QR,过Q作QN⊥AR,
∴∠PQD=45°,
∵∠QPR=180°-75°-45°=60°,且PQ=PR,
∴△PQR为等边三角形,
即PR=QR,
∵∠PQR=45°
∴∠RQN=15°=∠ARP,
在△NQR和△ARP中,
,
∴△NQR≌△ARP(AAS),
∴QN=RA,即AB=c.
 解:连接QR,过Q作QN⊥AR,
解:连接QR,过Q作QN⊥AR,∴∠PQD=45°,
∵∠QPR=180°-75°-45°=60°,且PQ=PR,
∴△PQR为等边三角形,
即PR=QR,
∵∠PQR=45°
∴∠RQN=15°=∠ARP,
在△NQR和△ARP中,
|
∴△NQR≌△ARP(AAS),
∴QN=RA,即AB=c.
点评:本题考查了全等三角形的判定和全等三角形对应边相等的性质,考查了等边三角形的判定和各边长相等的性质,本题中求证△NQR≌△ARP是解题的关键.

练习册系列答案
相关题目
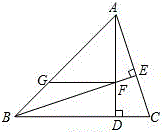 已知在△ABC中,∠ABC=45°,高AD所在的直线与高BE所在的直线交于点F,过点F作GF∥BC,交直线AB于点G,连接CF.
已知在△ABC中,∠ABC=45°,高AD所在的直线与高BE所在的直线交于点F,过点F作GF∥BC,交直线AB于点G,连接CF.
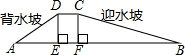 如图是一个拦水坝的横截面示意图,坝全长为30m,坝面宽为3m,迎水坡的坡度为1:3,背水坡度为1:2,堆砌水坝用去土方2325m3,则坝高DE=
如图是一个拦水坝的横截面示意图,坝全长为30m,坝面宽为3m,迎水坡的坡度为1:3,背水坡度为1:2,堆砌水坝用去土方2325m3,则坝高DE= 如图,已知AB∥CD,GH是直线,∠1+∠2=180°,问CD与EF是否平行?为什么?
如图,已知AB∥CD,GH是直线,∠1+∠2=180°,问CD与EF是否平行?为什么? 如图,已知点A的坐标为(-3,-4),点B的坐标为(5,0).
如图,已知点A的坐标为(-3,-4),点B的坐标为(5,0).