题目内容
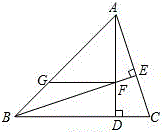 已知在△ABC中,∠ABC=45°,高AD所在的直线与高BE所在的直线交于点F,过点F作GF∥BC,交直线AB于点G,连接CF.
已知在△ABC中,∠ABC=45°,高AD所在的直线与高BE所在的直线交于点F,过点F作GF∥BC,交直线AB于点G,连接CF.(1)△ABC锐角三角形时,求证:AD=GF+CD;
(2)当∠BAC是钝角时.
①写出线段AD、CD、GF三者之间数量关系.(不必写出证明过程,直接写出结论);
②当BE=FE,BD=4时,求FG的长.
考点:全等三角形的判定与性质
专题:
分析:(1)易证AD=BD,∠DBF=∠CAD,即可证明△ACD≌△BFD,可得DF=DC,根据AD=AF+DF即可解题;
(2)①易证AD=BD,∠DBF=∠CAD,即可证明△ACD≌△BFD,可得DF=DC,根据AF=AD+DF即可解题;
②易证AE垂直平分BF,可得AB=AF,根据BD可求得AB的长,即可解题.
(2)①易证AD=BD,∠DBF=∠CAD,即可证明△ACD≌△BFD,可得DF=DC,根据AF=AD+DF即可解题;
②易证AE垂直平分BF,可得AB=AF,根据BD可求得AB的长,即可解题.
解答:证明:(1)∵∠ABD=45°,AD⊥BD,
∴AD=BD,
∵FG∥BC,
∴AF=FG,
∵∠DBF+∠BFD=90°,∠AFE+∠CAD=90°,∠AFE=∠BFD,
∴∠DBF=∠CAD,
在△ACD和△BFD中,
,
∴△ACD≌△BFD(ASA),
∴DF=DC,
∵AD=AF+DF,
∴AD=GF+CD;
(2)①作出图形,
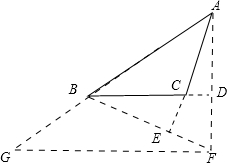
∵∠ABD=45°,AD⊥BD,
∴AD=BD,
∵FG∥BC,
∴AF=FG,
∵∠DBF+∠BFD=90°,∠AFE+∠CAD=90°,∠AFE=∠BFD,
∴∠DBF=∠CAD,
在△ACD和△BFD中,
,
∴△ACD≌△BFD(ASA),
∴DF=DC,
∵AF=AD+DF,
∴FG=AD+CD;
②∵BE=EF,AE⊥BF,
∴AE垂直平分BF,
∴AB=AF,
∵BD=4,
∴AB=4
,
∴FG=AF=AB=4
.
∴AD=BD,
∵FG∥BC,
∴AF=FG,
∵∠DBF+∠BFD=90°,∠AFE+∠CAD=90°,∠AFE=∠BFD,
∴∠DBF=∠CAD,
在△ACD和△BFD中,
|
∴△ACD≌△BFD(ASA),
∴DF=DC,
∵AD=AF+DF,
∴AD=GF+CD;
(2)①作出图形,

∵∠ABD=45°,AD⊥BD,
∴AD=BD,
∵FG∥BC,
∴AF=FG,
∵∠DBF+∠BFD=90°,∠AFE+∠CAD=90°,∠AFE=∠BFD,
∴∠DBF=∠CAD,
在△ACD和△BFD中,
|
∴△ACD≌△BFD(ASA),
∴DF=DC,
∵AF=AD+DF,
∴FG=AD+CD;
②∵BE=EF,AE⊥BF,
∴AE垂直平分BF,
∴AB=AF,
∵BD=4,
∴AB=4
| 2 |
∴FG=AF=AB=4
| 2 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ACD≌△BFD是解题的关键.

练习册系列答案
相关题目
下列不能作为直角三角形三边的是( )
| A、3,4,5 |
| B、5,12,13 |
| C、8,15,17 |
| D、5,6,7 |
已知a>0,那么|
-2a|可化简为( )
| a2 |
| A、-a | B、a | C、-3a | D、3a |
 如图,在半径为10的⊙O中,AB、CD是互相垂直的两条相等的弦,垂足为P,若OP=6
如图,在半径为10的⊙O中,AB、CD是互相垂直的两条相等的弦,垂足为P,若OP=6| 2 |
| A、12 | B、14 | C、16 | D、18 |
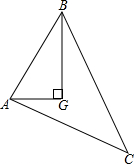 如图所示,点G是△ABC的重心,GA⊥GB,AB=5,则AC2+BC2的值为
如图所示,点G是△ABC的重心,GA⊥GB,AB=5,则AC2+BC2的值为 如图,∠AOB是直角,∠BOC=50°,OM平分∠AOC,ON平分∠BOC,则∠MON的度数为
如图,∠AOB是直角,∠BOC=50°,OM平分∠AOC,ON平分∠BOC,则∠MON的度数为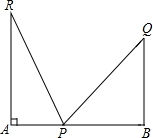 如图,设在一个宽度为AB的小巷内,一个梯子的长度为b,梯子的底部位于P点,当梯子靠在左面墙上时,顶端距底面的高为c,且梯子与底面的夹角为75°;靠在另一面墙上时,顶端距底面的高度为d,且梯子与底面的夹角为45°,求小巷的宽度AB.
如图,设在一个宽度为AB的小巷内,一个梯子的长度为b,梯子的底部位于P点,当梯子靠在左面墙上时,顶端距底面的高为c,且梯子与底面的夹角为75°;靠在另一面墙上时,顶端距底面的高度为d,且梯子与底面的夹角为45°,求小巷的宽度AB.