题目内容
 如图,已知点A的坐标为(-3,-4),点B的坐标为(5,0).
如图,已知点A的坐标为(-3,-4),点B的坐标为(5,0).(1)试说明OA=OB.
(2)求△AOB的面积.
(3)求原点到AB的距离.
考点:两点间的距离公式,三角形的面积
专题:计算题
分析:(1)根据两点间的距离公式求出OA和OB的长,即得到OA=OB;
(2)利用三角形面积公式求解;
(3)先根据两点间的距离公式计算出AB,然后利用面积法求原点到AB的距离.
(2)利用三角形面积公式求解;
(3)先根据两点间的距离公式计算出AB,然后利用面积法求原点到AB的距离.
解答:解:(1)∵A点坐标为(-3,-4),
∴OA=
=5,
∵点B的坐标为(5,0),
∴OB=5,
∴OA=OB;
(2)S△AOB=
•5•4=10;
(3)设原点到AB的距离为h,
∵AB=
=4
,
而S△AOB=
AB•h,
∴
•4
•h=10,
解得h=
,
即原点到AB的距离为
.
∴OA=
| (0+3)2+(0+4)2 |
∵点B的坐标为(5,0),
∴OB=5,
∴OA=OB;
(2)S△AOB=
| 1 |
| 2 |
(3)设原点到AB的距离为h,
∵AB=
| (-3-5)2+(-4-0)2 |
| 5 |
而S△AOB=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 5 |
解得h=
| 5 |
即原点到AB的距离为
| 5 |
点评:本题考查了两点间的距离公式:设有两点A(x1,y1),B(x2,y2),则这两点间的距离为AB=
.
| (x1-x2)2+(y1-y2)2 |

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 如图所示,长方形由大小不一的正方形组成,原来的长方形的周长为68cm,那么原来长方形的长为( )
如图所示,长方形由大小不一的正方形组成,原来的长方形的周长为68cm,那么原来长方形的长为( )| A、18cm | B、20cm |
| C、16cm | D、22cm |
 如图,∠AOB是直角,∠BOC=50°,OM平分∠AOC,ON平分∠BOC,则∠MON的度数为
如图,∠AOB是直角,∠BOC=50°,OM平分∠AOC,ON平分∠BOC,则∠MON的度数为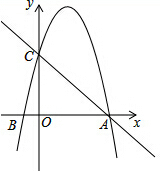 如图,抛物线y=-x2+3x+4的图象交x轴于A,B,交y轴于C,点P是抛物线的一点,若以△ACP是以AC为直角边的直角三角形,求点P的坐标.
如图,抛物线y=-x2+3x+4的图象交x轴于A,B,交y轴于C,点P是抛物线的一点,若以△ACP是以AC为直角边的直角三角形,求点P的坐标.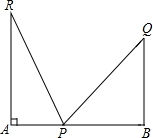 如图,设在一个宽度为AB的小巷内,一个梯子的长度为b,梯子的底部位于P点,当梯子靠在左面墙上时,顶端距底面的高为c,且梯子与底面的夹角为75°;靠在另一面墙上时,顶端距底面的高度为d,且梯子与底面的夹角为45°,求小巷的宽度AB.
如图,设在一个宽度为AB的小巷内,一个梯子的长度为b,梯子的底部位于P点,当梯子靠在左面墙上时,顶端距底面的高为c,且梯子与底面的夹角为75°;靠在另一面墙上时,顶端距底面的高度为d,且梯子与底面的夹角为45°,求小巷的宽度AB.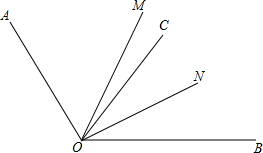 如图,OM平分∠AOB,OC是∠AOB内部的一条射线,ON平分∠BOC,有以下说法:
如图,OM平分∠AOB,OC是∠AOB内部的一条射线,ON平分∠BOC,有以下说法: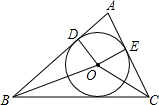 如图所示,⊙O是△ABC的内切圆,切AB、AC于点D、E.
如图所示,⊙O是△ABC的内切圆,切AB、AC于点D、E.