题目内容
13.(1)已知$\frac{a+3b}{a}=2$,则$\frac{b}{a}$=$\frac{1}{3}$;(2)已知$\frac{1}{a}-\frac{1}{b}=5$,则$\frac{3a-5ab-3b}{a-3ab-b}$=$\frac{5}{2}$.
分析 (1)已知等式逆用同分母分式的加法法则变形,即可求出所求式子的值;
(2)已知等式左边通分并利用同分母分式的减法法则计算,整理得到a-b=-5ab,原式变形后代入计算即可求出值.
解答 解:(1)由$\frac{a+3b}{a}$=2,得到1+3•$\frac{b}{a}$=2,
则$\frac{b}{a}$=$\frac{1}{3}$;
(2)由$\frac{1}{a}$-$\frac{1}{b}$=5,得到$\frac{b-a}{ab}$=5,即a-b=-5ab,
则原式=$\frac{3(a-b)-5ab}{a-b-3ab}$=$\frac{-15ab-5ab}{-5ab-3ab}$=$\frac{5}{2}$,
故答案为:(1)$\frac{1}{3}$;(2)$\frac{5}{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
4.关于x的方程2x+5a=3的解与方程2x+2=0的解相同,则a的值是( )
| A. | 4 | B. | 1 | C. | $\frac{1}{5}$ | D. | -1 |
1.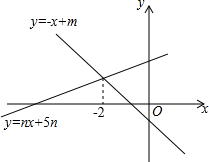 如图,直线y=-x+m与直线y=nx+5n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+5n>0的整数解为( )
如图,直线y=-x+m与直线y=nx+5n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+5n>0的整数解为( )
 如图,直线y=-x+m与直线y=nx+5n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+5n>0的整数解为( )
如图,直线y=-x+m与直线y=nx+5n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+5n>0的整数解为( )| A. | -5,-4,-3 | B. | -4,-3 | C. | -4,-3,-2 | D. | -3,-2 |
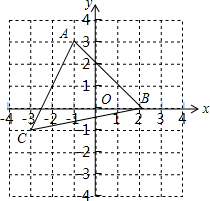 如图,在平面直角坐标系中有一个△ABC,顶点A(-1,3),B(2,0),C(-3,-1).
如图,在平面直角坐标系中有一个△ABC,顶点A(-1,3),B(2,0),C(-3,-1).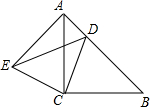 如图,∠ACB=∠ECD=90°,AC=BC,EC=DC,点D在AB边上.
如图,∠ACB=∠ECD=90°,AC=BC,EC=DC,点D在AB边上.