题目内容
4.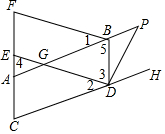 如图,已知点E,F为四边形ABDC的边CA的延长线上的两点,连接DE,BF,作∠BDH的平分线DP交AB的延长线于点P.若∠1=∠2,∠3=∠4,∠5=∠C.
如图,已知点E,F为四边形ABDC的边CA的延长线上的两点,连接DE,BF,作∠BDH的平分线DP交AB的延长线于点P.若∠1=∠2,∠3=∠4,∠5=∠C.(1)判断DE与BF是否平行?并说明理由;
(2)试说明:∠C=2∠P.
分析 (1)根据平行线的判定得出BD∥CE,根据平行线的性质得出∠5=∠FAB,求出∠C=∠FAB,根据平行线的判定得出AB∥CD,根据平行线的性质得出∠2=∠BGD即可;
(2)求出∠BDP=∠PDH=∠P,根据三角形的外角性质得出即可.
解答 解:(1)DE∥BF,
理由是:∵∠3=∠4,
∴BD∥CE,
∴∠5=∠FAB,
∵∠5=∠C,
∴∠C=∠FAB,
∴AB∥CD,
∴∠2=∠BGD,
∵∠1=∠2,
∴∠1=∠BGD,
∴DE∥BF;
(2)∵AB∥CD,
∴∠P=∠PDH,
∵DP平分∠BDH,
∴∠BDP=∠PDH,
∴∠BDP=∠PDH=∠P,
∵∠5=∠P+∠BDP,
∴∠5=2∠P,
∵∠C=∠5,
∴∠C=2∠P.
点评 本题考查了平行线的性质和判定、三角形外角性质,能熟练地运用定理进行推理是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.

练习册系列答案
相关题目
12.已知$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$是方程组$\left\{\begin{array}{l}{2x+(m-1)y=2}\\{nx+y=1}\end{array}\right.$的解,则(m+n)2017的值为( )
| A. | 22017 | B. | -1 | C. | 1 | D. | 0 |
14.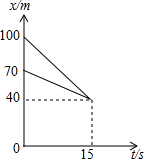 在动画片《喜羊羊与灰太狼》中,有一次灰太狼追赶喜羊羊,在距羊村40m处追上了喜羊羊,如图中s表示它们与羊村的距离(单位:m),t表示时间(单位:s),根据相关信息判断,下列说法中错误的是( )
在动画片《喜羊羊与灰太狼》中,有一次灰太狼追赶喜羊羊,在距羊村40m处追上了喜羊羊,如图中s表示它们与羊村的距离(单位:m),t表示时间(单位:s),根据相关信息判断,下列说法中错误的是( )
 在动画片《喜羊羊与灰太狼》中,有一次灰太狼追赶喜羊羊,在距羊村40m处追上了喜羊羊,如图中s表示它们与羊村的距离(单位:m),t表示时间(单位:s),根据相关信息判断,下列说法中错误的是( )
在动画片《喜羊羊与灰太狼》中,有一次灰太狼追赶喜羊羊,在距羊村40m处追上了喜羊羊,如图中s表示它们与羊村的距离(单位:m),t表示时间(单位:s),根据相关信息判断,下列说法中错误的是( )| A. | 灰太狼追上喜羊羊时,喜羊羊跑了60m | |
| B. | 喜羊羊与灰太狼最初的距离是30m | |
| C. | 灰太狼跑了60m追上了喜羊羊 | |
| D. | 灰太狼用15s追上了喜羊羊 |
 如图,△ABD是等腰直角三角形,点C是BD延长线上一点,F在AC上,AD=AF,E为△ADC内一点,连接AE,BE,AE平分∠CAD,AE⊥BE.
如图,△ABD是等腰直角三角形,点C是BD延长线上一点,F在AC上,AD=AF,E为△ADC内一点,连接AE,BE,AE平分∠CAD,AE⊥BE.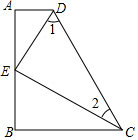 如图,已知AD⊥AB,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°,那么BC⊥AB,说明理由.
如图,已知AD⊥AB,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°,那么BC⊥AB,说明理由.