题目内容
5. 如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C;直线DF分别交l1、l2、l3于点D、E、F,若AB=3,BC=4,DE=2,则线段EF的长为$\frac{8}{3}$.
如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C;直线DF分别交l1、l2、l3于点D、E、F,若AB=3,BC=4,DE=2,则线段EF的长为$\frac{8}{3}$.
分析 利用平行线分线段成比例定理得到$\frac{AB}{BC}$=$\frac{DE}{EF}$,然后把AB=3,BC=4,DE=2代入计算即可.
解答 解:∵l1∥l2∥l3,
∴$\frac{AB}{BC}$=$\frac{DE}{EF}$,即$\frac{3}{4}$=$\frac{2}{EF}$,
∴EF=$\frac{8}{3}$.
故答案为$\frac{8}{3}$.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.

练习册系列答案
相关题目
17.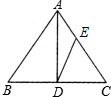 如图,已知AD是等腰△ABC底边上的高,且sinB=$\frac{4}{5}$.点E在AC上且AE:EC=2:3.则tan∠ADE等于( )
如图,已知AD是等腰△ABC底边上的高,且sinB=$\frac{4}{5}$.点E在AC上且AE:EC=2:3.则tan∠ADE等于( )
 如图,已知AD是等腰△ABC底边上的高,且sinB=$\frac{4}{5}$.点E在AC上且AE:EC=2:3.则tan∠ADE等于( )
如图,已知AD是等腰△ABC底边上的高,且sinB=$\frac{4}{5}$.点E在AC上且AE:EC=2:3.则tan∠ADE等于( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
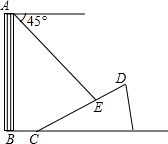 如图,一楼房AB后有一假山,其斜坡CD坡比为1:$\sqrt{3}$,山坡坡面上点E处有一休息亭,测得假山坡脚C与楼房水平距离BC=6米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.
如图,一楼房AB后有一假山,其斜坡CD坡比为1:$\sqrt{3}$,山坡坡面上点E处有一休息亭,测得假山坡脚C与楼房水平距离BC=6米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.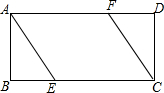 如图,E、F分别是矩形ABCD的边BC、AD上的点,且BE=DF
如图,E、F分别是矩形ABCD的边BC、AD上的点,且BE=DF 如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴、y轴上一点B在第一象限,函数y=$\frac{k}{x}(x>0)$的图象经过BC边上的点M,且MB=2MC,若矩形OABC的面积为6,则k的值为2.
如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴、y轴上一点B在第一象限,函数y=$\frac{k}{x}(x>0)$的图象经过BC边上的点M,且MB=2MC,若矩形OABC的面积为6,则k的值为2. 如图,某高楼CD与处地面垂直,要在高楼前的地面A处安装某种射灯,安装后,射灯发出的光线与地面的最大夹角∠DAC为70°,光线与地面的最小夹角∠DAB为35°,要使射灯发光时照射在高楼上的区域宽BC为50米,求A处到高楼的距离AD.(结果精确到0.1米)
如图,某高楼CD与处地面垂直,要在高楼前的地面A处安装某种射灯,安装后,射灯发出的光线与地面的最大夹角∠DAC为70°,光线与地面的最小夹角∠DAB为35°,要使射灯发光时照射在高楼上的区域宽BC为50米,求A处到高楼的距离AD.(结果精确到0.1米) 如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE.
如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE.