题目内容
14.已知一个口袋中装有7个只有颜色不同的球,其中3个白球,4个黑球.(1)求从中随机抽取出一个黑球的概率是多少?
(2)若往口袋中再放入x个白球和y个黑球,从口袋中随机取出一个白球的概率是$\frac{1}{4}$,求y与x之间的函数关系式.
(3)若在(2)的条件下,放入白球x的范围是0<x<4(x为整数),求y的最大值.
分析 (1)根据概率求法:符合条件的情况数目除以全部情况的总数列式求得答案;
(2)根据白球的概率公式得到相应的方程求解即可;
(3)利用一次函数的性质得出最大值即可.
解答 解:(1)取出一个黑球的概率$P=\frac{4}{3+4}=\frac{4}{7}$;
(2)∵取出一个白球的概率$P=\frac{3+x}{7+x+y}$,
∴$\frac{3+x}{7+x+y}=\frac{1}{4}$,
∴12+4x=7+x+y,
∴y与x的函数关系式为:y=3x+5.
(3)∵k=3>0,
∴y随x的增大而增大,y有最大值.
∴x=3时,y有最大值是,y最大=3×3+5=14.
点评 此题考查一次函数的性质,掌握一次函数的性质与概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$是解决问题的关键.

练习册系列答案
相关题目
4.关于x的方程x2-2x+c=0有两个相等的实数根,则c的值为( )
| A. | 1 | B. | -1 | C. | 4 | D. | -4 |
5. 如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C;直线DF分别交l1、l2、l3于点D、E、F,若AB=3,BC=4,DE=2,则线段EF的长为$\frac{8}{3}$.
如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C;直线DF分别交l1、l2、l3于点D、E、F,若AB=3,BC=4,DE=2,则线段EF的长为$\frac{8}{3}$.
 如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C;直线DF分别交l1、l2、l3于点D、E、F,若AB=3,BC=4,DE=2,则线段EF的长为$\frac{8}{3}$.
如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C;直线DF分别交l1、l2、l3于点D、E、F,若AB=3,BC=4,DE=2,则线段EF的长为$\frac{8}{3}$.
9.下列等式成立的是( )
| A. | (a+4)(a-4)=a2-4 | B. | 2a2-3a=-a | C. | a6÷a3=a2 | D. | (a2)3=a6 |
3.下列方程中是一元二次方程的是( )
| A. | x+2y=1 | B. | 2x(x-1)=2x2+3 | C. | x2-2=0 | D. | 3x+$\frac{1}{x}$=4 |
4.1-$\sqrt{15}$的值( )
| A. | 比-2大 | B. | 比-3大 | C. | 比-3小 | D. | 比-4小 |
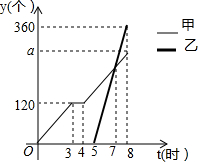 某天,甲组工人加工零件,工作中有一次停产检修机器,然后继续加工.由于任务紧急,乙组工人加入,与甲组工人一起生产零件.两组各自加工零件的数量y(个)与甲组工人加工时间t(时)之间的函数图象如图所示.
某天,甲组工人加工零件,工作中有一次停产检修机器,然后继续加工.由于任务紧急,乙组工人加入,与甲组工人一起生产零件.两组各自加工零件的数量y(个)与甲组工人加工时间t(时)之间的函数图象如图所示.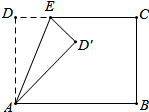 如图,在矩形ABCD中,AD=5,AB=8,点E为DC边上的一个动点,把△ADE沿AE折叠,当点D的对应点刚好D落在矩形ABCD的对称轴上时,则DE的长为$\frac{5}{2}$或$\frac{5\sqrt{3}}{3}$.
如图,在矩形ABCD中,AD=5,AB=8,点E为DC边上的一个动点,把△ADE沿AE折叠,当点D的对应点刚好D落在矩形ABCD的对称轴上时,则DE的长为$\frac{5}{2}$或$\frac{5\sqrt{3}}{3}$.