题目内容
15.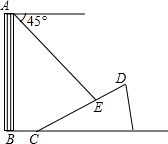 如图,一楼房AB后有一假山,其斜坡CD坡比为1:$\sqrt{3}$,山坡坡面上点E处有一休息亭,测得假山坡脚C与楼房水平距离BC=6米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.
如图,一楼房AB后有一假山,其斜坡CD坡比为1:$\sqrt{3}$,山坡坡面上点E处有一休息亭,测得假山坡脚C与楼房水平距离BC=6米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.(1)求点E距水平面BC的高度;
(2)求楼房AB的高.(结果精确到0.1米,参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
分析 (1)过点E作EF⊥BC于点F.在Rt△CEF中,求出CF=$\sqrt{3}$EF,然后根据勾股定理解答;
(2)过点E作EH⊥AB于点H.在Rt△AHE中,∠HAE=45°,结合(1)中结论得到CF的值,再根据AB=AH+BH,求出AB的值.
解答 解:(1)过点E作EF⊥BC于点F.
在Rt△CEF中,CE=20,$\frac{EF}{CF}=\frac{1}{\sqrt{3}}$,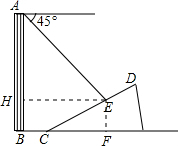
∴EF2+($\sqrt{3}$EF)2=202,
∵EF>0,
∴EF=10.
答:点E距水平面BC的高度为10米.
(2)过点E作EH⊥AB于点H.
则HE=BF,BH=EF.
在Rt△AHE中,∠HAE=45°,
∴AH=HE,
由(1)得CF=$\sqrt{3}$EF=10$\sqrt{3}$(米)
又∵BC=6米,
∴HE=6+10$\sqrt{3}$米,
∴AB=AH+BH=6+10$\sqrt{3}$+10=16+10$\sqrt{3}$≈33.3(米).
答:楼房AB的高约是33.3米.
点评 本题考查了解直角三角形的应用--仰角俯角问题、坡度坡角问题,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
20.七年级有6个班,每个班平均有n个学生,并且七年级一共有30位老师,则七年级共有师生( )人.
| A. | (6n+30)人 | B. | (6n-30)人 | C. | (30-6n)人 | D. | 6n人 |
4.关于x的方程x2-2x+c=0有两个相等的实数根,则c的值为( )
| A. | 1 | B. | -1 | C. | 4 | D. | -4 |
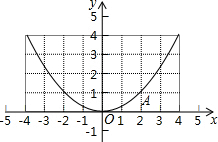 如图是一个二次函数的图象,顶点是原点O,且过点A(2,1),
如图是一个二次函数的图象,顶点是原点O,且过点A(2,1),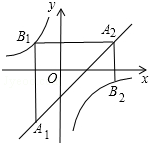 如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-$\frac{1}{x}$ 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2016=$\frac{1}{2}$.
如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-$\frac{1}{x}$ 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2016=$\frac{1}{2}$.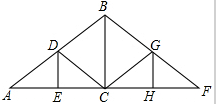 如图是屋架设计图的一部分,其中∠A=30°,点D是斜梁AB的中点,BC、DE垂直于横梁AC,AB=8m,则立柱BC,DE要多长?
如图是屋架设计图的一部分,其中∠A=30°,点D是斜梁AB的中点,BC、DE垂直于横梁AC,AB=8m,则立柱BC,DE要多长? 如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C;直线DF分别交l1、l2、l3于点D、E、F,若AB=3,BC=4,DE=2,则线段EF的长为$\frac{8}{3}$.
如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C;直线DF分别交l1、l2、l3于点D、E、F,若AB=3,BC=4,DE=2,则线段EF的长为$\frac{8}{3}$.