题目内容
11.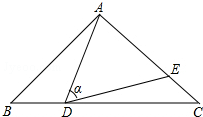 如图,在△ABC中,AB=AC=5,点D是边BC上一动点(不与B,C重合),
如图,在△ABC中,AB=AC=5,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且sinα=$\frac{3}{5}$.下列结论:
①△ADE∽△ACD;
②当BD=2时,△ABD与△DCE全等;
③△DCE为直角三角形时,BD的长一定为4;
④0<CE≤3.2.
其中正确的结论是①④.(把你认为正确结论的序号都填上)
分析 ①根据有两组对应角相等的三角形相似即可证明;
②由BD=2,则DC=5,证得对应边不相等,△ABD与△DCE不全等;
③分两种情况讨论,通过三角形相似即可求得;
④作AG⊥BC于G,如图,根据等腰三角形的性质得BG=CG,再利用余弦的定义计算出BG=8,则BC=2BG=16,设BD=x,则CD=16-x,证明△ABD∽△DCE,利用相似比可表示出CE=-$\frac{1}{5}$x2+$\frac{8}{5}$x,然后利用二次函数的性质求CE的最大值,于是得到结论.
解答 解:①∵AB=AC,
∴∠B=∠C,
又∵∠ADE=∠B
∴∠ADE=∠C,
∴△ADE∽△ACD;
故①正确,
②作AG⊥BC于G,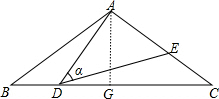
∵AB=AC=5,∠ADE=∠B=α,sinα=$\frac{3}{5}$,
∴cosB=cosα=$\sqrt{1-sinα}$=$\frac{4}{5}$,
∴BG=ABcosB,
∴BC=2BG=2ABcosB=2×5×$\frac{4}{5}$=8,
∵BD=2,
∴DC=6,
∴AB≠DC,
∴△ABD与△DCE不全等,故②错误,
③当∠AED=90°时,由①可知:△ADE∽△ACD,
∴∠ADC=∠AED,
∵∠AED=90°,
∴∠ADC=90°,
即AD⊥BC,
∵AB=AC,
∴BD=CD,
∴∠ADE=∠B=α且cosα=$\frac{4}{5}$,AB=5,
∴BD=4,
当∠CDE=90°时,易△CDE∽△BAD,
∵∠CDE=90°,
∴∠BAD=90°,
∵∠B=α且cosα=$\frac{4}{5}$,AB=5,
∴cosB=$\frac{AB}{BD}$=$\frac{4}{5}$,
∴BD=$\frac{25}{4}$.
故③错误.
∵AG⊥BC于G,如图,
∵AB=AC,
∴BG=CG,
∵∠ADE=∠B=α,
∴cosB=cosα=$\frac{BG}{AB}$=$\frac{4}{5}$,
∴BG=$\frac{4}{5}$×5=4,
∴BC=2BG=8,
设BD=x,则CD=8-x,
∵∠ADC=∠B+∠BAD,即α+∠CDE=∠B+∠BAD,
∴∠CDE=∠BAD,
而∠B=∠C,
∴△ABD∽△DCE,
∴$\frac{AB}{CD}$=$\frac{BD}{CE}$,即$\frac{5}{8-x}$=$\frac{x}{CE}$,
∴CE=-$\frac{1}{5}$x2+$\frac{8}{5}$x
=-$\frac{1}{5}$(x-4)2+3.2,
当x=4时,CE最大,最大值为3.2.
∴0<CE≤3.2.故④正确.
故答案为:①④.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,三角函数,二次函数的最大值问题,熟练掌握相似三角形的判定和性质是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\sqrt{12}$ | B. | $\sqrt{7}$ | C. | $\frac{1}{{\sqrt{3}}}$ | D. | $\sqrt{\frac{1}{2}}$ |
| A. | 等腰梯形对角线相等 | |
| B. | 一组对边平行另一组对边相等的四边形是平行四边形 | |
| C. | 矩形的对角线相等 | |
| D. | 对角线互相垂直且相等的四边形是正方形 |
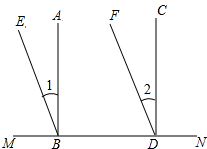
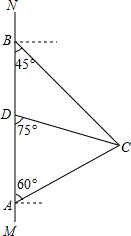 如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距$50(\sqrt{3}+1)$海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距$50(\sqrt{3}+1)$海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.