题目内容
20.如图1,在正方形ABCD中,以点A为顶点的∠MAN=45°,其中AM交DC于E,AN交BC于F.(1)求证:BF+DE=EF;
(2)如图2,将∠MAN绕点A旋转,使AM交DC的延长线于E,AN交CB的延长线于F,请探索BF、DE、EF的关系,并说明理由.

分析 (1)从结论的结构上看,证明的是线段的和差关系,需要截长补短,又根据90度夹45度的已知条件,不难度想到将三角形ADE顺时针旋转90度至ABG,再证明三角形AGF与三角形AEF全等即可;
(2)同(1)类似,只不过此时DE最长,只需将三角形ABF逆时针旋转90度至ADG,然后证明三角形AFE与三角形AGE全等即可.
解答 (1)证明:将△ADE顺时针旋转90度至△ABG,如图1,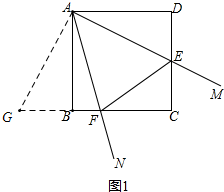
则AG=AE,∠GAB=∠EAD,BG=DE
∵∠EAF=45°,∠BAD=90°,
∴∠BAF+∠EAD=45°,
∴∠GAB+∠BAF=45°,
∴∠GAF=∠EAF,
在△GAF和△EAF中,
$\left\{\begin{array}{l}{AG=AE}\\{∠GAF=∠EAF}\\{AF=AF}\end{array}\right.$,
∴△GAF≌△EAF(SAS),
∴EF=GF=BG+BF=DE+BF;
(2)解:将△ABF逆时针旋转90度至△ADG,如图2,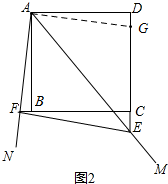
则AG=AF,DG=BF,∠FAB=∠GAD,
∵∠FAB+∠FAE=∠EAF=45°,
∴∠GAD+∠BAE=45°,
∴∠GAE=45°,
在△FAE和△GAE中,
$\left\{\begin{array}{l}{AF=AG}\\{∠FAE=∠GAE}\\{AE=AE}\end{array}\right.$,
∴△FAE≌△GAE(SAS),
∴EF=GE,
∴DE=DG+GE=BF+EF.
点评 本题主要考查了全等三角形的判定与性质,正方形的性质、旋转的应用,难度中等.值得注意的是,本题出现的90度夹45度模型是高频考点,务必掌握其处理技巧和证明方法.

练习册系列答案
相关题目
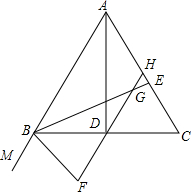 已知,在△ABC中,AB=AC,AD、BE分别是△ABC的角平分线,H为AC的中点,连接HD,交BE于G,BF平分∠MBC,交HD的延长线于F.
已知,在△ABC中,AB=AC,AD、BE分别是△ABC的角平分线,H为AC的中点,连接HD,交BE于G,BF平分∠MBC,交HD的延长线于F.
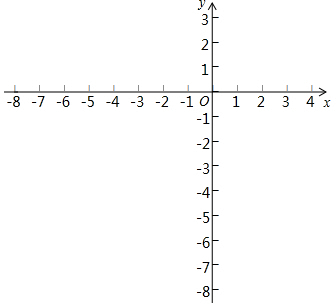 已知:平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).
已知:平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).