题目内容
5.(1)若$\frac{x}{3}=\frac{y}{5}=\frac{z}{7}$,求$\frac{x-y+z}{x+y-z}$的值;(2)若$\frac{a+2}{3}=\frac{b}{4}=\frac{c+5}{6}$,且2a-b+3c=21,求a:b:c.
分析 (1)设比值为k,然后用k表示出x、y、z,再代入代数式即可解答;
(2)设比值为k,然后用k表示出a、b、c,再代入等式求出k值,然后相比即可.
解答 解:(1)设$\frac{x}{3}=\frac{y}{5}=\frac{z}{7}=k$,
∴x=3k,y=5k,z=7k,
∴$\frac{x-y+z}{x+y-z}=\frac{3k-5k+7k}{3k+5k-7k}=\frac{5k}{k}$=5;
(2)设$\frac{a+2}{3}=\frac{b}{4}=\frac{c+5}{6}$=k,
则a=3k-2,b=4k,c=6k-5,
所以,2(3k-2)-4k+3(6k-5)=21,
解得k=2,
所以a=6-2=4,b=8,c=7,
所以a:b:c=4:8:7.
点评 本题考查了比例的性质,利用“设k法”表示出a、b、c是解决本题的关键.

练习册系列答案
相关题目
10.某地一周内每天的最高气温与最低气温记录如下表,通过观察与计算,你会发现:周日的温差最大,周一的温差最小.
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 最高气温 | 10℃ | 12℃ | 11℃ | 9℃ | 7℃ | 5℃ | 7℃ |
| 最低气温 | 2℃ | 1℃ | 0℃ | -1℃ | -4℃ | -5℃ | -5℃ |
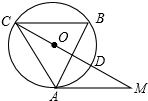 如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.求证:CD=2DM.
如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.求证:CD=2DM.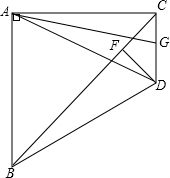 如图,△ABC是等腰直角三角形,∠BAC=90°,△ABD是等边三角形,D、C两点在直线AB同侧,连接CD交AB延长线于E,AG⊥DC于G,DF⊥CB于F.
如图,△ABC是等腰直角三角形,∠BAC=90°,△ABD是等边三角形,D、C两点在直线AB同侧,连接CD交AB延长线于E,AG⊥DC于G,DF⊥CB于F.
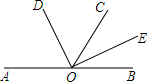 如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.若∠BOC=62°,求∠DOE的度数.
如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.若∠BOC=62°,求∠DOE的度数. 如图,∠1+∠2+∠3+∠4的值为360°.
如图,∠1+∠2+∠3+∠4的值为360°. 如图,已知,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿AB以4cm/s的速度向点B运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.
如图,已知,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿AB以4cm/s的速度向点B运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.