题目内容
8.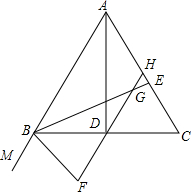 已知,在△ABC中,AB=AC,AD、BE分别是△ABC的角平分线,H为AC的中点,连接HD,交BE于G,BF平分∠MBC,交HD的延长线于F.
已知,在△ABC中,AB=AC,AD、BE分别是△ABC的角平分线,H为AC的中点,连接HD,交BE于G,BF平分∠MBC,交HD的延长线于F.(1)求证:DG=DB;
(2)请判断四边形BGCF的形状,并说明理由.
分析 (1)若要证明DG=DB可证∠BGD=∠GBD,根据题意知DH是△ABC中位线即DH∥AB得∠BGD=∠GBA,根据BE平分∠ABC得∠GBA=∠GBD,从而得证;
(2)与(1)同理可证DB=DF,又DB=DG可知DG=DF,由BE平分∠ABC、BF平分∠MBC可知∠FBG=90°,根据有一个角是直角且对角线互相平分的四边形是矩形可得.
解答 解:(1)∵AB=AC,AD平分∠BAC,
∴BD=BC,
∵H为AC的中点,
∴DH∥AB,且DH=$\frac{1}{2}$AB,
∴∠BGD=∠GBA,
又∵BE平分∠ABC,
∴∠GBA=∠GBD=$\frac{1}{2}$∠ABC,
∴∠BGD=∠GBD,
∴DG=DB;
(2)四边形BGCF是矩形,
由(1)知,FH∥AB,
∴∠MBF=∠F,
又∵BF平分∠MBC,
∴∠MBF=∠DBF=$\frac{1}{2}$∠MBC
∴∠F=∠DBF,
∴DB=DF,
又∵DB=DG,
∴DG=DF,
∵BD=BC,∠GBD=$\frac{1}{2}$∠ABC,∠DBF=$\frac{1}{2}$∠MBC
∴BC、FG互相平分,且∠FBG=∠FBD+∠GBD=$\frac{1}{2}$(∠ABC+∠MBC)=90°,
故四边形BGCF是矩形.
点评 本题主要考查等腰三角形的性质及角平分线的运用能力,通过证明两角相等得到对应的边相等是解题的关键.

练习册系列答案
相关题目
6.关于函数y=-$\frac{2}{3}$x2的性质描述错误的是( )
| A. | 它的图象关于y轴对称 | |
| B. | 该抛物线开口向下 | |
| C. | 原点是该抛物线上的最高点 | |
| D. | 当x为任意实数时,函数值y总是负数 |
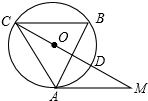 如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.求证:CD=2DM.
如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.求证:CD=2DM.
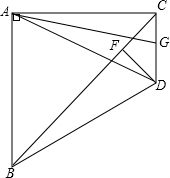 如图,△ABC是等腰直角三角形,∠BAC=90°,△ABD是等边三角形,D、C两点在直线AB同侧,连接CD交AB延长线于E,AG⊥DC于G,DF⊥CB于F.
如图,△ABC是等腰直角三角形,∠BAC=90°,△ABD是等边三角形,D、C两点在直线AB同侧,连接CD交AB延长线于E,AG⊥DC于G,DF⊥CB于F.
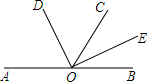 如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.若∠BOC=62°,求∠DOE的度数.
如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.若∠BOC=62°,求∠DOE的度数.