题目内容
 如图,已知坐标系中点A(2,-1),B(7,-1),C(3,-3).
如图,已知坐标系中点A(2,-1),B(7,-1),C(3,-3).(1)判定△ABC的形状;
(2)设△ABC关于x轴的对称图形是△A1B1C1,若把△A1B1C1的各顶点的横坐标都加2.纵坐标不变,则△A1B1C1的位置发生什么变化?若最终位置是△A2B2C2,求C2点的坐标;
(3)x轴上有一点P,使PC+PB最小,求PC+PB的最小值.
考点:作图-轴对称变换,轴对称-最短路线问题
专题:
分析:(1)计算出AC2,BC2,AB2,比较数量关系即可;
(2)把△A1B1C1的各顶点的横坐标都加2.纵坐标不变,则图形向右移动两个单位;
(3)连接CB1,与x轴的交点即为P,利用勾股定理求出CB1的长即可.
(2)把△A1B1C1的各顶点的横坐标都加2.纵坐标不变,则图形向右移动两个单位;
(3)连接CB1,与x轴的交点即为P,利用勾股定理求出CB1的长即可.
解答: 解:(1)∵AC2=22+12=5,BC2=42+22=20,AB2=52,
解:(1)∵AC2=22+12=5,BC2=42+22=20,AB2=52,
∴AC2+BC2=AB2,
∴△ABC是直角三角形;
(2)如图:C2坐标为(5,2);
(3)如图:连接CB1,与x轴的交点即为P.
CB1=
=4
.
 解:(1)∵AC2=22+12=5,BC2=42+22=20,AB2=52,
解:(1)∵AC2=22+12=5,BC2=42+22=20,AB2=52,∴AC2+BC2=AB2,
∴△ABC是直角三角形;
(2)如图:C2坐标为(5,2);
(3)如图:连接CB1,与x轴的交点即为P.
CB1=
| 42+42 |
| 2 |
点评:本题考查了作图--轴对称变换和最短路径问题,熟悉轴对称的性质和勾股定理是解题的关键.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
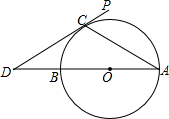 如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,若OB=BD,则∠A的大小是( )
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,若OB=BD,则∠A的大小是( )| A、30° | B、32° |
| C、34° | D、36° |
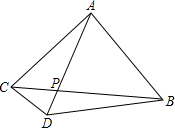 如图所示,在△ABC中,∠BAC=90°,AB=AC=AD,AD交BC于点P,∠CAD=30°,AC=6,求:
如图所示,在△ABC中,∠BAC=90°,AB=AC=AD,AD交BC于点P,∠CAD=30°,AC=6,求: