题目内容
 如图,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,点D、E在x轴上,CF交y轴于点B(0,2),且矩形其面积为8,此抛物线的解析式.
如图,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,点D、E在x轴上,CF交y轴于点B(0,2),且矩形其面积为8,此抛物线的解析式.考点:待定系数法求二次函数解析式
专题:计算题
分析:由抛物线的顶点为A(0,1)得到抛物线的对称轴为y轴,则可判断C、F点为抛物线上的对称点,再根据矩形的面积得到CF=4,则可得到F点的坐标为(2,2),然后设顶点式y=ax2+1,再把F(2,2)代入求出a的值即可.
解答:解:∵抛物线的顶点为A(0,1),
∴抛物线的对称轴为y轴,
∵四边形CDEF为矩形,
∴C、F点为抛物线上的对称点,
∵矩形其面积为8,OB=2
∴CF=4,
∴F点的坐标为(2,2),
设抛物线解析式为y=ax2+1,
把F(2,2)代入得4a+1=2,解得a=
,
∴抛物线解析式为y=
x2+1.
∴抛物线的对称轴为y轴,
∵四边形CDEF为矩形,
∴C、F点为抛物线上的对称点,
∵矩形其面积为8,OB=2
∴CF=4,
∴F点的坐标为(2,2),
设抛物线解析式为y=ax2+1,
把F(2,2)代入得4a+1=2,解得a=
| 1 |
| 4 |
∴抛物线解析式为y=
| 1 |
| 4 |
点评:本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
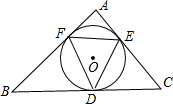 如图,△ABC的内切圆⊙O与各边相切于点D、E、F,且∠FOD=∠EOD=135°,则△ABC一定不是( )
如图,△ABC的内切圆⊙O与各边相切于点D、E、F,且∠FOD=∠EOD=135°,则△ABC一定不是( )| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
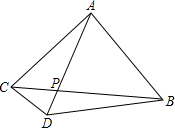 如图所示,在△ABC中,∠BAC=90°,AB=AC=AD,AD交BC于点P,∠CAD=30°,AC=6,求:
如图所示,在△ABC中,∠BAC=90°,AB=AC=AD,AD交BC于点P,∠CAD=30°,AC=6,求: