题目内容
 已知:E是正方形ABCD的边长AD上一点,BF平分∠EBC,交CD于F,求证:BE=AE+CF.
已知:E是正方形ABCD的边长AD上一点,BF平分∠EBC,交CD于F,求证:BE=AE+CF.考点:全等三角形的判定与性质
专题:证明题
分析:把△ABE绕点B顺时针旋转90°,AB与BC重合,再根据条件证明∠GBF=∠BFG可得到BG=GF,可证得结论.
解答: 证明:
证明:
如图,将△ABE绕B点旋转,使AB和BC重合,
设△BCG是旋转后的△ABE,
∴△ABE≌△CBG,
∴AE=CG,BE=BG,∠ABE=∠CBG,
∵BF是∠EBC的角平分线,
∴∠EBF=∠FBC,
∴∠ABE+∠EBF=∠GBC+∠FBC,
∴∠ABF=∠FBG,
∵正方形ABCD,
∴AB∥CD,
∴∠ABF=∠BFG,
∴∠GBF=∠BFG,
∴BG=GF,
∵GF=CG+CF=AE+CF,BG=BE,
∴BE=AE+CF.
 证明:
证明:如图,将△ABE绕B点旋转,使AB和BC重合,
设△BCG是旋转后的△ABE,
∴△ABE≌△CBG,
∴AE=CG,BE=BG,∠ABE=∠CBG,
∵BF是∠EBC的角平分线,
∴∠EBF=∠FBC,
∴∠ABE+∠EBF=∠GBC+∠FBC,
∴∠ABF=∠FBG,
∵正方形ABCD,
∴AB∥CD,
∴∠ABF=∠BFG,
∴∠GBF=∠BFG,
∴BG=GF,
∵GF=CG+CF=AE+CF,BG=BE,
∴BE=AE+CF.
点评:本题主要考查正方形的性质及等腰三角形的判定和性质,把AE和CF移到同一条线段上,再证明该线段与BE相等是解题的关键.证明线段的和差关系时主要就是截或接.

练习册系列答案
相关题目
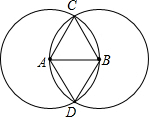 如图,分别为线段AB的两个端点A、B为圆心,以线段AB为半径画圆,两圆交于C、D两点,则下列判断中正确的是( )
如图,分别为线段AB的两个端点A、B为圆心,以线段AB为半径画圆,两圆交于C、D两点,则下列判断中正确的是( )| A、△ABC和△ABD都一定是等边三角形 |
| B、△ABC和△ABD都不一定是等边三角形 |
| C、△ABC不一定是等边三角形 |
| D、△ABD不一定是等边三角形 |
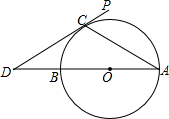 如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,若OB=BD,则∠A的大小是( )
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,若OB=BD,则∠A的大小是( )| A、30° | B、32° |
| C、34° | D、36° |
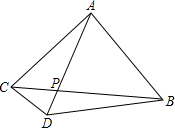 如图所示,在△ABC中,∠BAC=90°,AB=AC=AD,AD交BC于点P,∠CAD=30°,AC=6,求:
如图所示,在△ABC中,∠BAC=90°,AB=AC=AD,AD交BC于点P,∠CAD=30°,AC=6,求: