题目内容
2.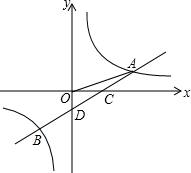 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知A(3,1),点B的坐标为(m,-2).
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知A(3,1),点B的坐标为(m,-2).(1)直接写出反比例函数的解析式;
(2)求一次函数的解析式;
(3)在y轴上是否存在一点P,使得△PDC与△CDO相似?若存在求P点的坐标,若不存在说明理由.
分析 (1)把A坐标代入反比例解析式求出k的值,即可确定出反比例解析式;
(2)把B坐标代入反比例解析式求出m的值,确定出B坐标,由A与B坐标,利用待定系数法确定出直线AB解析式即可;
(3)在y轴上,存在一点P,使得△PDC与△CDO相似,理由为:过点C作CP⊥AB,交y轴于点P,如图所示,根据直线AB解析式确定出C与D坐标,得到OC,OD,DC的长,由三角形PDC与三角形CDO相似,得比例求出PD的长,由DP-OD求出OP的长,即可确定出P坐标.
解答 解:(1)把A(1,3)代入反比例解析式得:3=$\frac{k}{1}$,即k=3,
则反比例解析式为y=$\frac{3}{x}$;
(2)∵B(m,-2)在反比例函数y=$\frac{3}{x}$上,
∴-2=$\frac{3}{m}$,即m=-$\frac{3}{2}$,即B(-$\frac{3}{2}$,-2),
把A与B坐标代入一次函数解析式得:$\left\{\begin{array}{l}{3a+b=1}\\{-\frac{3}{2}a+b=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{2}{3}}\\{b=-1}\end{array}\right.$,
则一次函数解析式为y=$\frac{2}{3}$x-1;
(3)在y轴上存在一点P,使得△PDC与△CDO相似,理由为:
过点C作CP⊥AB,交y轴于点P,如图所示,
∵C、D两点在直线y=$\frac{2}{3}$x-1上,
∴C、D的坐标分别为C($\frac{3}{2}$,0),D(0,-1),
∴OC=$\frac{3}{2}$,OD=1,DC=$\frac{\sqrt{13}}{2}$,
∵△PDC∽△CDO,
∴$\frac{PD}{CD}$=$\frac{CD}{DO}$,即$\frac{PD}{\frac{\sqrt{13}}{2}}$=$\frac{\frac{\sqrt{13}}{2}}{1}$,
解得:PD=$\frac{13}{4}$,
∴OP=DP-OD=$\frac{13}{4}$-1=$\frac{9}{4}$,
则点P的坐标为(0,$\frac{9}{4}$).
点评 此题属于反比例函数综合题,涉及的知识有:待定系数法确定反比例解析式与一次函数解析式,相似三角形的性质,以及坐标与图形性质,熟练掌握待定系数法是解本题的关键.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案| A. | -10<y<-5 | B. | -2<y<-1 | C. | 5<y<10 | D. | y>10 |
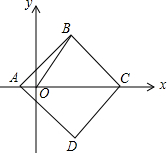 如图,在平面直角坐标系中,O为坐标原点,正方形ABCD的对角线AC落在x轴上,A(-1,0),C(7,0),连接OB,则∠BOC的正弦值为( )
如图,在平面直角坐标系中,O为坐标原点,正方形ABCD的对角线AC落在x轴上,A(-1,0),C(7,0),连接OB,则∠BOC的正弦值为( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
| A. | 10,26,24 | B. | 16,10,6 | C. | 30,17,8 | D. | 24,13,5 |
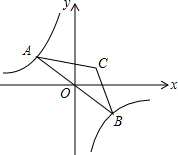 如图,点A是双曲线y=-$\frac{9}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值为3.
如图,点A是双曲线y=-$\frac{9}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值为3.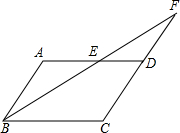 如图,在?ABCD中,AB=4,AD=7,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF的长是( )
如图,在?ABCD中,AB=4,AD=7,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF的长是( )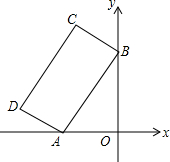 如图,矩形ABCD的两个顶点A,B在坐标轴上,AD:AB=1:2,且A(-2,0),∠BAO=60°,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过该矩形的顶点,则k=-2-$\sqrt{3}$或-6-$\sqrt{3}$.
如图,矩形ABCD的两个顶点A,B在坐标轴上,AD:AB=1:2,且A(-2,0),∠BAO=60°,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过该矩形的顶点,则k=-2-$\sqrt{3}$或-6-$\sqrt{3}$.